题目
(2) ^2-2x+1leqslant 0
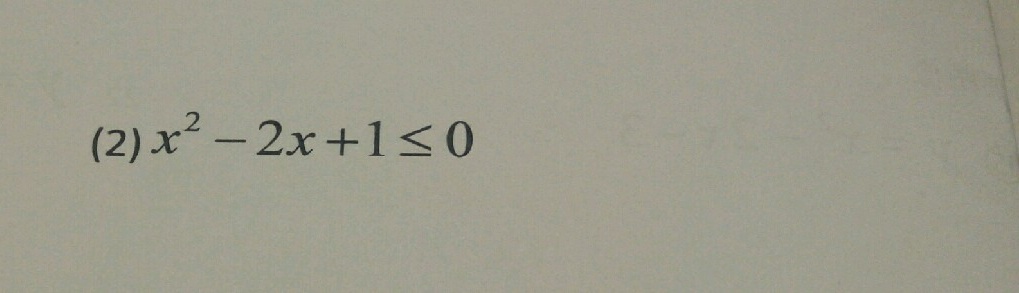
题目解答
答案

解析
考查要点:本题主要考查二次不等式的解法,特别是利用完全平方公式将二次三项式转化为平方形式,并结合平方数的非负性求解。
解题核心思路:
- 识别完全平方结构:观察到二次项、一次项和常数项满足$a^2 - 2ab + b^2$的形式,可直接写成$(a - b)^2$。
- 利用平方数的非负性:任何实数的平方均非负,因此不等式$(x - 1)^2 \leq 0$的解只能是平方等于0的情况。
破题关键点:
- 正确分解因式:将$x^2 - 2x + 1$分解为$(x - 1)^2$。
- 理解平方数的性质:明确平方数的最小值为0,从而确定唯一解。
步骤1:因式分解
原不等式为:
$x^2 - 2x + 1 \leq 0$
观察二次项、一次项和常数项,发现其符合完全平方公式:
$x^2 - 2x + 1 = (x - 1)^2$
因此,原不等式可化简为:
$(x - 1)^2 \leq 0$
步骤2:分析平方数的性质
根据数学基本性质,任何实数的平方均大于或等于0,即:
$(x - 1)^2 \geq 0$
结合不等式$(x - 1)^2 \leq 0$,可知只有当平方等于0时,才能同时满足两个不等式。因此:
$x - 1 = 0 \quad \Rightarrow \quad x = 1$
结论:
唯一满足条件的解是$x = 1$。