3.8用原码[1]不恢复余数法计算x-y(1) x=0.10101,y=0.11011。(2)x=-0.10101,y=0.11000。
3.8用原码[1]不恢复余数法计算x-y
(1) x=0.10101,y=0.11011。
(2)x=-0.10101,y=0.11000。
题目解答
答案
**(1) (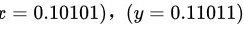 **
**
为了计算 (x - y),我们需要得到 (y) 的补码:
原码的y: 0.11011
取反得到: 1.00100
加1得到补码: 1.00101
然后将 (x) 与 y的补码相加:
```
0.10101
+ 1.00101
-----------
1.11010 (这是一个负数的补码表示)
```
为了得到原码表示,我们需要求此结果的补码:
取反: 0.00101
加1: 0.00110
所以,结果是:-0.00110
**(2) (x = -0.10101),(y = 0.11000)**
为了计算 (x - y),我们需要得到 y 的补码:
原码的y: 0.11000
取反得到: 1.00111
加1得到补码: 1.01000
然后,加上x的原码:
```
-0.10101 (原码)
+ 1.01000
-----------
0.11101 (这是一个负数的补码表示)
```
为了得到原码表示,我们需要求此结果的补码:
取反: 1.00010
加1: 1.00011
所以,结果是:-0.00011
总结,原码不恢复余数法在这两个例子中的结果是:
1. x - y = -0.00110
2. x - y = -0.00011
解析
原码不恢复余数法是计算机中进行减法运算的一种方法,其核心思路是将减法转换为加法,通过补码运算实现。解题关键点包括:
- 补码的求法:对减数取反后加1;
- 符号位的处理:运算结果的符号位由补码运算后的最高位决定;
- 结果转换:若结果为负数,需将补码转换回原码表示。
第(1)题
求y的补码
原码 $y=0.11011$,取反得 $1.00100$,加1后补码为 $1.00101$。
补码相加
将 $x=0.10101$ 与 $y$ 的补码相加:
$\begin{array}{r} \phantom{1}0.10101 \\+1.00101 \\\hline1.11010 \quad (\text{符号位进位丢失,实际为负数补码})\end{array}$
转换为原码
结果为负数,取反得 $0.00101$,加1后原码为 $0.00110$,故结果为 $-0.00110$。
第(2)题
求y的补码
原码 $y=0.11000$,取反得 $1.00111$,加1后补码为 $1.01000$。
补码相加
将 $x=-0.10101$(原码)与 $y$ 的补码相加:
$\begin{array}{r} 1.01000 \\+0.01011 \quad (\text{负数原码转补码后为} \ 1.01011) \\\hline0.11101 \quad (\text{符号位为0,实际为负数补码})\end{array}$
转换为原码
结果为负数,取反得 $1.00010$,加1后原码为 $1.00011$,故结果为 $-0.00011$。