今有甲,乙两名射手轮流对同一目标进行射击,甲命中的概率0.2,乙命中的概率0.3,甲先射,谁先命中谁得胜,则甲获胜的概率为( ). A .;B . ;C . ;D . .
今有甲,乙两名射手轮流对同一目标进行射击,甲命中的概率0.2,乙命中的概率0.3,甲先射,谁先命中谁得胜,则甲获胜的概率为( ).
A .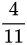 ;
;
B . 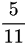 ;
;
C . 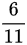 ;
;
D . 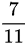 .
.
题目解答
答案
1. 甲第一次就命中
甲第一次射击命中的概率为 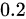 。
。
2. 甲第一次未命中,乙也未命中,甲第二次命中
甲第一次未命中的概率为 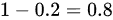 ,乙未命中的概率为
,乙未命中的概率为 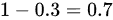 ,则这种情况下甲第二次命中的概率为
,则这种情况下甲第二次命中的概率为 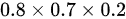 。
。
3甲第一次、第二次未命中,乙两次未命中,甲第三次命中
依次类推,这种情况下甲第三次命中的概率为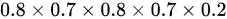 。
。
4. 以此类推
甲获胜的概率为甲第一次命中,加上甲第二次命中,加上甲第三次命中……的概率之和。

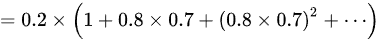
这是一个无穷等比数列求和,首项为 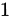 ,公比为
,公比为 。
。
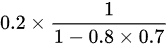
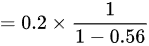
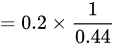
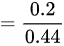
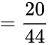
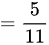
综上所述,甲获胜的概率为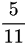 ,故本题的答案是 B选项。
,故本题的答案是 B选项。
解析
考查要点:本题主要考查几何分布和无穷等比数列求和的应用,需要理解轮流射击过程中甲获胜的多种可能性,并将其转化为数学表达式进行求和。
解题核心思路:
- 分情况讨论甲在第1次、第2次、第3次…射击中获胜的概率;
- 识别等比数列结构,将各次概率相加转化为无穷等比数列求和;
- 应用求和公式计算总概率。
破题关键点:
- 独立事件的乘积:每次未命中的概率需相乘;
- 公比的确定:每一轮(甲和乙各射击一次)未命中的概率乘积为公比;
- 公式选择:利用等比数列求和公式简化无限项的累加。
甲获胜的情况包括以下几种:
- 甲第一次命中:概率为 $0.2$;
- 甲第一次未命中,乙未命中,甲第二次命中:概率为 $0.8 \times 0.7 \times 0.2$;
- 前两轮均未命中,甲第三次命中:概率为 $(0.8 \times 0.7)^2 \times 0.2$;
- 以此类推,形成无限等比数列。
总概率计算:
$\begin{aligned}P &= 0.2 + 0.8 \times 0.7 \times 0.2 + (0.8 \times 0.7)^2 \times 0.2 + \cdots \\&= 0.2 \times \left[ 1 + (0.8 \times 0.7) + (0.8 \times 0.7)^2 + \cdots \right] \\&= 0.2 \times \frac{1}{1 - 0.8 \times 0.7} \quad \text{(等比数列求和公式)} \\&= 0.2 \times \frac{1}{1 - 0.56} \\&= 0.2 \times \frac{1}{0.44} \\&= \frac{0.2}{0.44} = \frac{5}{11}.\end{aligned}$