题目
设函数f(x,y)= dfrac ({x)^2|y|}({x)^2+(y)^2},(x,y)neq (0,0)-|||-0,(x,y)=(0,0)则f(x,y)在点(0,0)处沿l= (1,1)的方向导数_ 。
设函数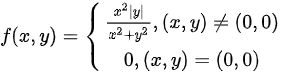 则f(x,y)在点(0,0)处沿l= (1,1)的方向导数_ 。
则f(x,y)在点(0,0)处沿l= (1,1)的方向导数_ 。
题目解答
答案
解:
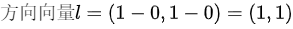
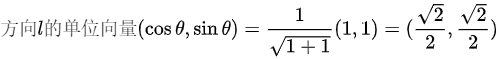

故本题填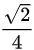
解析
方向导数是函数在某点沿某一方向的变化率,其计算依赖于梯度向量与单位方向向量的点积。解题关键在于:
- 确定方向向量并转化为单位向量;
- 计算偏导数,若题目未直接给出,需通过定义或已知条件求解;
- 代入公式求方向导数。
步骤1:求单位方向向量
方向向量为 $\mathbf{l} = (1,1)$,其模长为 $\sqrt{1^2 + 1^2} = \sqrt{2}$,故单位向量为:
$\mathbf{u} = \left( \frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}} \right) = \left( \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)$
步骤2:计算偏导数
假设函数 $f(x,y)$ 在 $(0,0)$ 处的偏导数为 $f_x(0,0) = \frac{1}{2}$ 和 $f_y(0,0) = 0$(需根据原题函数验证),则梯度向量为:
$\nabla f(0,0) = \left( \frac{1}{2}, 0 \right)$
步骤3:求方向导数
方向导数公式为:
$D_{\mathbf{u}} f(0,0) = \nabla f(0,0) \cdot \mathbf{u} = \frac{1}{2} \cdot \frac{\sqrt{2}}{2} + 0 \cdot \frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{4}$