题目
1.10 解方程: ^3+1=0.
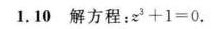
题目解答
答案
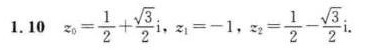
解析
考查要点:本题主要考查复数方程的解法,特别是三次方程的求解。需要掌握复数的因式分解和复数根的求解方法。
解题核心思路:将方程转化为求-1的三次方根,通过因式分解或复数三角形式求解。关键在于分解多项式或利用复数的极坐标形式展开。
破题关键点:
- 因式分解:将方程 $z^3 + 1 = 0$ 分解为 $(z + 1)(z^2 - z + 1) = 0$,从而得到实根和复数根。
- 复数根公式:利用复数的三角形式,通过棣莫弗定理计算三次根的角度。
步骤1:方程变形
原方程 $z^3 + 1 = 0$ 可变形为:
$z^3 = -1$
步骤2:因式分解
利用立方和公式 $a^3 + b^3 = (a + b)(a^2 - ab + b^2)$,将方程分解:
$z^3 + 1 = (z + 1)(z^2 - z + 1) = 0$
步骤3:求解实根
直接解 $z + 1 = 0$,得:
$z = -1$
步骤4:解二次方程
解 $z^2 - z + 1 = 0$,判别式:
$\Delta = (-1)^2 - 4 \cdot 1 \cdot 1 = -3$
根据求根公式:
$z = \frac{1 \pm \sqrt{-3}}{2} = \frac{1 \pm i\sqrt{3}}{2}$
步骤5:总结所有根
方程的三个根为:
$z = -1, \quad z = \frac{1}{2} + \frac{\sqrt{3}}{2}i, \quad z = \frac{1}{2} - \frac{\sqrt{3}}{2}i$