题目
某地警察每晚查获机动车酒驾的人数X服从参数为A=23的泊松分布,则今晚该地警察查获至少一人酒驾的概率为______.
某地警察每晚查获机动车酒驾的人数X服从参数为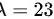 的泊松分布,则今晚该地警察查获至少一人酒驾的概率为______.
的泊松分布,则今晚该地警察查获至少一人酒驾的概率为______.
题目解答
答案
X服从参数为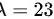 的泊松分布,则X的分布律为
的泊松分布,则X的分布律为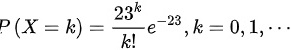 ,
,
则今晚该地警察查获至少一人酒驾的概率为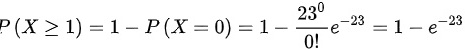 .
.
解析
泊松分布是描述单位时间内事件发生次数的概率分布,其参数$\lambda$表示平均发生次数。本题中,查获酒驾人数$X$服从参数$\lambda=23$的泊松分布,要求计算“至少查获一人”的概率。
关键思路:
-
补集思想:计算“至少一人”的概率,等价于1减去“零人”的概率,即$P(X \geq 1) = 1 - P(X=0)$。
-
泊松分布公式:$P(X=k) = \dfrac{\lambda^k}{k!} e^{-\lambda}$,其中$k=0,1,2,\dots$。
-
简化计算:当$k=0$时,公式简化为$P(X=0) = e^{-\lambda}$。
-
确定目标概率:
题目要求$P(X \geq 1)$,根据补集思想,转化为:
$P(X \geq 1) = 1 - P(X=0).$ -
计算$P(X=0)$:
代入泊松分布公式,当$k=0$时:
$P(X=0) = \dfrac{23^0}{0!} e^{-23} = \dfrac{1}{1} e^{-23} = e^{-23}.$ -
最终结果:
代入补集公式得:
$P(X \geq 1) = 1 - e^{-23}.$