题目
方程^4-3(x)^3+6x-4=0-|||-__的整数解的个数是( )。A、0B、1C、2D、3
方程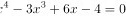 的整数解的个数是( )。
的整数解的个数是( )。
- A、0
- B、1
- C、2
- D、3
题目解答
答案
C. 2
解析
考查要点:本题主要考查多项式方程的整数解求解方法,涉及有理根定理的应用和多项式因式分解。
解题核心思路:
- 确定可能的整数根:根据有理根定理,可能的整数根是常数项因数(±1, ±2, ±4)与首项系数因数(1)的比值,即±1, ±2, ±4。
- 代入验证:逐一试根,找到整数解后,通过多项式除法分解原方程,逐步降低次数,直至找到所有整数解。
破题关键点:
- 试根法快速锁定整数解。
- 因式分解将高次方程转化为低次方程,简化求解过程。
步骤1:确定可能的整数根
根据有理根定理,可能的整数根为±1, ±2, ±4。
步骤2:代入验证
- x=1:
$1^4 - 3 \cdot 1^3 + 6 \cdot 1 - 4 = 1 - 3 + 6 - 4 = 0$
x=1是解。 - x=2:
$2^4 - 3 \cdot 2^3 + 6 \cdot 2 - 4 = 16 - 24 + 12 - 4 = 0$
x=2是解。 - 其余值(如x=-1, x=4等)代入后均不满足方程。
步骤3:因式分解
- 分解原方程:
用综合除法将原方程分解为:
$(x-1)(x^3 - 2x^2 - 2x + 4) = 0$ - 分解三次多项式:
再次用综合除法分解三次多项式为:
$(x-2)(x^2 - 2) = 0$
最终原方程分解为:
$(x-1)(x-2)(x^2 - 2) = 0$
步骤4:确定整数解
解得:
- $x=1$(整数)
- $x=2$(整数)
- $x=\sqrt{2}$(非整数)
- $x=-\sqrt{2}$(非整数)
整数解共2个。