题目
求曲线 =(x-1)sqrt [3]({x)^2} 的凹凸区间和拐点.
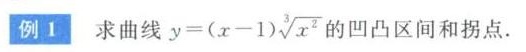
题目解答
答案

解析
步骤 1:求一阶导数
首先,将给定的函数 $y=(x-1)\sqrt [3]{{x}^{2}}$ 重写为 $y={x}^{\dfrac {5}{3}}-{x}^{\dfrac {2}{3}}$。然后,求一阶导数 $y'$。
$$
y'=\dfrac {5}{3}{x}^{\dfrac {2}{3}}-\dfrac {2}{3}{x}^{-\dfrac {1}{3}}
$$
步骤 2:求二阶导数
接着,求二阶导数 $y''$。
$$
y''=\dfrac {10}{9}{x}^{-\dfrac {1}{3}}+\dfrac {2}{9}{x}^{-\dfrac {4}{3}}=\dfrac {2(5x+1)}{9{x}^{\dfrac {4}{3}}}
$$
步骤 3:确定拐点
令 $y''=0$,解得 $x=-\dfrac {1}{5}$。又当 $x=0$ 时,$y''$ 不存在。因此,需要讨论 $x$ 在 $(-\infty ,-\dfrac {1}{5})$,$(-\dfrac {1}{5},0)$,$(0,+\infty )$ 三个区间内的符号。
步骤 4:确定凹凸区间
根据 $y''$ 的符号,确定曲线的凹凸区间。当 $y''>0$ 时,曲线是凹的;当 $y''<0$ 时,曲线是凸的。
首先,将给定的函数 $y=(x-1)\sqrt [3]{{x}^{2}}$ 重写为 $y={x}^{\dfrac {5}{3}}-{x}^{\dfrac {2}{3}}$。然后,求一阶导数 $y'$。
$$
y'=\dfrac {5}{3}{x}^{\dfrac {2}{3}}-\dfrac {2}{3}{x}^{-\dfrac {1}{3}}
$$
步骤 2:求二阶导数
接着,求二阶导数 $y''$。
$$
y''=\dfrac {10}{9}{x}^{-\dfrac {1}{3}}+\dfrac {2}{9}{x}^{-\dfrac {4}{3}}=\dfrac {2(5x+1)}{9{x}^{\dfrac {4}{3}}}
$$
步骤 3:确定拐点
令 $y''=0$,解得 $x=-\dfrac {1}{5}$。又当 $x=0$ 时,$y''$ 不存在。因此,需要讨论 $x$ 在 $(-\infty ,-\dfrac {1}{5})$,$(-\dfrac {1}{5},0)$,$(0,+\infty )$ 三个区间内的符号。
步骤 4:确定凹凸区间
根据 $y''$ 的符号,确定曲线的凹凸区间。当 $y''>0$ 时,曲线是凹的;当 $y''<0$ 时,曲线是凸的。