题目
设曲线=sqrt (x)与直线=sqrt (x)所围平面图形记为D，则D的面积，D绕x轴旋转一周而形成的旋转体体积分别为（ ）（A）=sqrt (x)（B）=sqrt (x)（C）=sqrt (x)（D）=sqrt (x)
设曲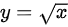线
与直线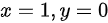
所围平面图形记为D，则D的面积，D绕x轴旋转一周而形成的旋转体体积分别为（ ）
（A）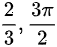
（B）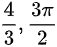
（C）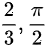
（D）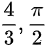
题目解答
答案
选C
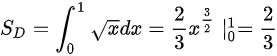
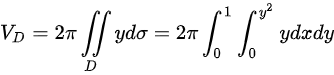
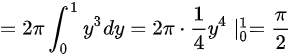
故选C
解析
步骤 1：计算平面图形D的面积
根据题目，平面图形D由曲线$y=\sqrt{x}$与直线$x=1$和$y=0$所围成。因此，D的面积可以通过计算曲线$y=\sqrt{x}$在区间$[0,1]$上的定积分得到。
步骤 2：计算旋转体体积
当平面图形D绕x轴旋转一周时，形成的旋转体体积可以通过计算曲线$y=\sqrt{x}$在区间$[0,1]$上的旋转体体积得到。旋转体体积的计算公式为$V=2\pi\int_{a}^{b}y^2dx$，其中$y=\sqrt{x}$，$a=0$，$b=1$。
根据题目，平面图形D由曲线$y=\sqrt{x}$与直线$x=1$和$y=0$所围成。因此，D的面积可以通过计算曲线$y=\sqrt{x}$在区间$[0,1]$上的定积分得到。
步骤 2：计算旋转体体积
当平面图形D绕x轴旋转一周时，形成的旋转体体积可以通过计算曲线$y=\sqrt{x}$在区间$[0,1]$上的旋转体体积得到。旋转体体积的计算公式为$V=2\pi\int_{a}^{b}y^2dx$，其中$y=\sqrt{x}$，$a=0$，$b=1$。