题目
研究下列函数的连续性,并画出函数的图形.(1) f(x)= ) (x)^2,0leqslant xleqslant 1 2-x,1lt xleqslant 2 ...
研究下列函数的连续性,并画出函数的图形.
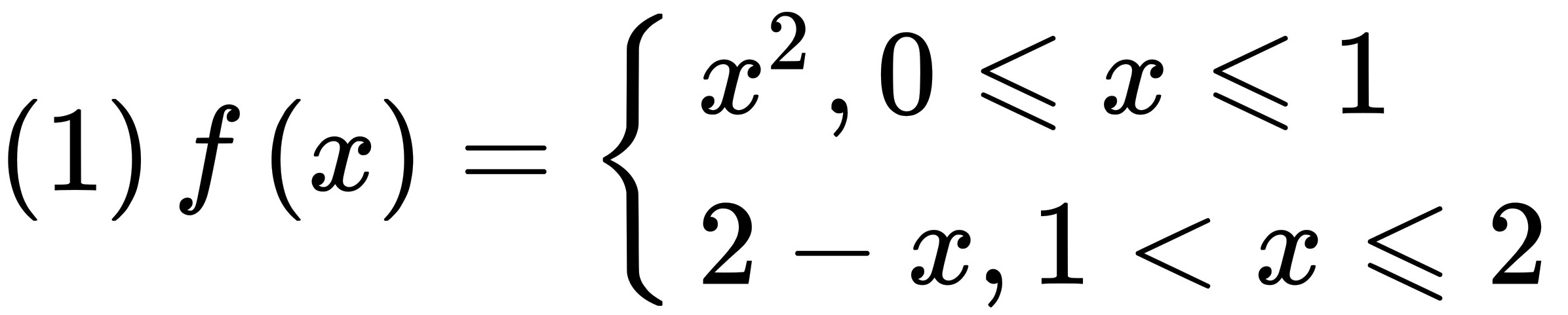 ;
;
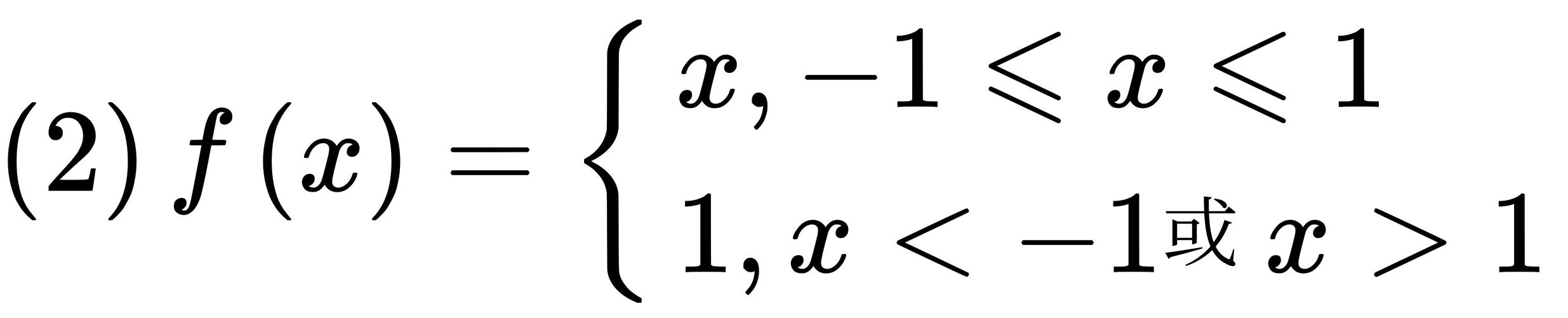 .
.
题目解答
答案
(1)作函数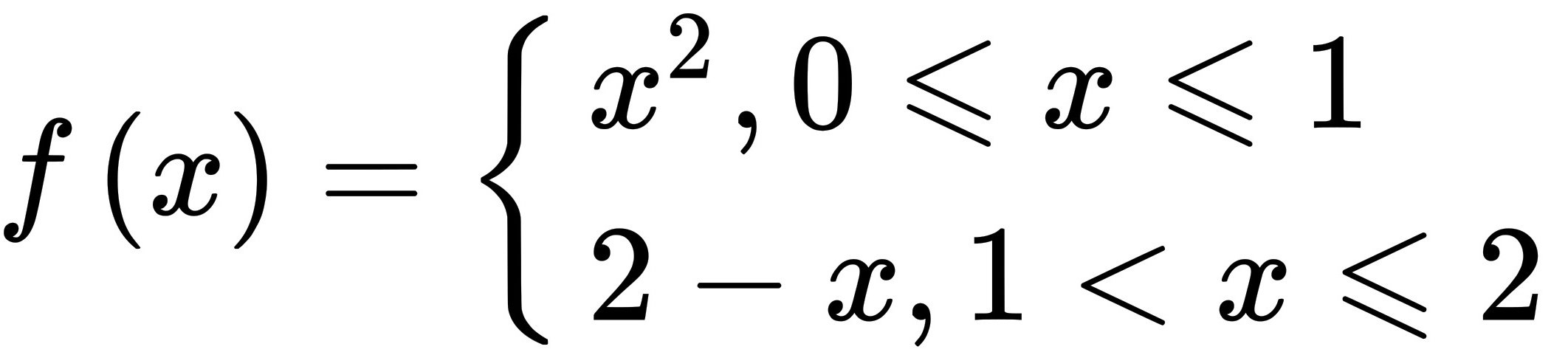 的图象如下,
的图象如下,
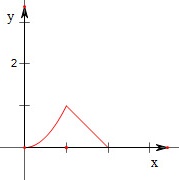
故函数在其定义域上连续;
(2)作函数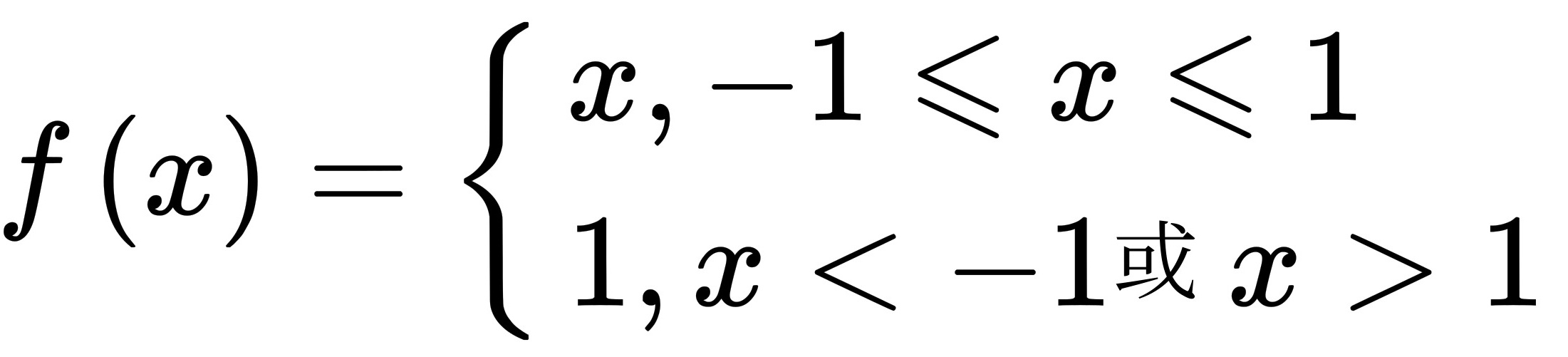 的图象如下,
的图象如下,
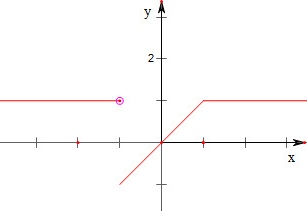
故函数在其定义域上不连续.
.解析
考查要点:分段函数的连续性判断及图形绘制。
解题思路:
- 分段点分析:对于分段函数,需重点检查各分段点处的左右极限是否相等,且是否等于函数值。
- 连续性判定:若所有分段点处连续,则函数在其定义域上连续;否则不连续。
- 图形绘制:根据分段表达式,分区间绘制对应函数图形,注意分段点的连接情况。
第(1)题
分段点:$x=1$
- 左极限:当$x \to 1^-$时,$f(x) = x^2 \to 1^2 = 1$。
- 右极限:当$x \to 1^+$时,$f(x) = 2 - x \to 2 - 1 = 1$。
- 函数值:$f(1) = 1^2 = 1$。
结论:左右极限相等且等于$f(1)$,故$x=1$处连续。
其他区间:$x^2$在$[0,1]$连续,$2-x$在$(1,2]$连续,因此函数在定义域$[0,2]$上连续。
图形绘制:
- $0 \leq x \leq 1$:抛物线$y = x^2$,从$(0,0)$到$(1,1)$。
- $1 < x \leq 2$:直线$y = 2 - x$,从$(1,1)$到$(2,0)$。
第(2)题
分段点:$x=-1$和$x=1$
-
$x=-1$处:
- 左极限:当$x \to -1^-$时,$f(x) = 1$。
- 右极限:当$x \to -1^+$时,$f(x) = x \to -1$。
- 函数值:$f(-1) = -1$。
结论:左极限$1 \neq$右极限$-1$,故$x=-1$处不连续。
-
$x=1$处:
- 左极限:当$x \to 1^-$时,$f(x) = x \to 1$。
- 右极限:当$x \to 1^+$时,$f(x) = 1$。
- 函数值:$f(1) = 1$。
结论:左右极限均为$1$,等于$f(1)$,故$x=1$处连续。
结论:因$x=-1$处不连续,函数在其定义域上不连续。
图形绘制:
- $x < -1$:水平线$y=1$。
- $-1 \leq x \leq 1$:直线$y=x$,从$(-1,-1)$到$(1,1)$。
- $x > 1$:水平线$y=1$。