题目
函数 =dfrac (1)({x)^2+1} 是 ()A、偶函数B、奇函数C、单调函数D、无界函数
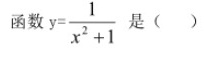
- A、偶函数
- B、奇函数
- C、单调函数
- D、无界函数
题目解答
答案
A. 偶函数
解析
考查要点:本题主要考查函数的基本性质,包括奇偶性、单调性、有界性等概念的理解与应用。
解题核心思路:
- 判断奇偶性:通过验证$f(-x)$与$f(x)$的关系,确定函数是否为偶函数或奇函数。
- 分析单调性:通过求导数并分析其符号变化,判断函数是否在整个定义域内单调。
- 判断有界性:通过分析函数值的范围,判断是否存在上下界。
破题关键点:
- 偶函数的定义:若$f(-x) = f(x)$,则函数为偶函数。
- 导数的符号变化:导数的正负变化表明函数在不同区间的增减趋势。
- 分母的最小值:分母$x^2 + 1$的最小值为1,直接决定函数的最大值。
选项A:偶函数
- 验证$f(-x)$:
$f(-x) = \frac{1}{(-x)^2 + 1} = \frac{1}{x^2 + 1} = f(x)$
因此,函数满足偶函数的定义。
选项B:奇函数
- 验证$f(-x)$与$-f(x)$的关系:
$f(-x) = f(x) \neq -f(x)$
因此,函数不是奇函数。
选项C:单调函数
- 求导数:
$y' = \frac{d}{dx} \left( \frac{1}{x^2 + 1} \right) = \frac{-2x}{(x^2 + 1)^2}$ - 分析导数符号:
- 当$x > 0$时,$y' < 0$,函数单调递减;
- 当$x < 0$时,$y' > 0$,函数单调递增。
因此,函数在定义域内不整体单调。
选项D:无界函数
- 分析函数值范围:
- 分母$x^2 + 1 \geq 1$,故$0 < \frac{1}{x^2 + 1} \leq 1$。
- 函数值始终在$(0, 1]$之间,有界。