题目
求函数 (x)=(x)^3-(x)^2-x+1 的凹凸区间和拐点
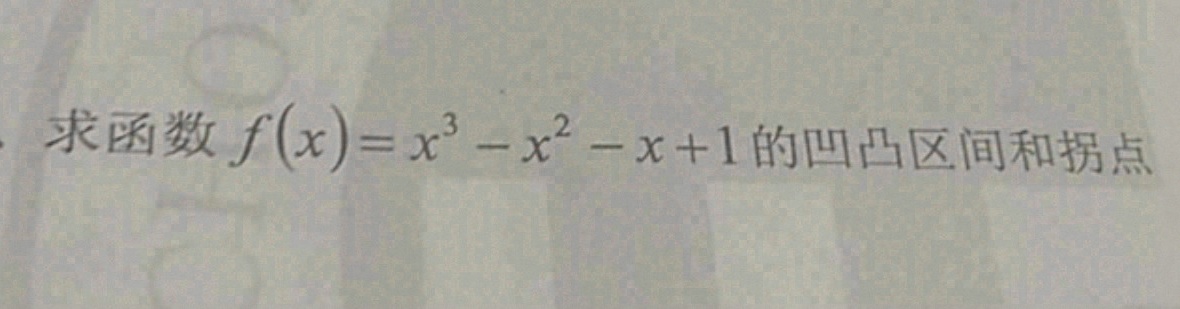
题目解答
答案

解析
步骤 1:求一阶导数
对函数 $f(x)={x}^{3}-{x}^{2}-x+1$ 求一阶导数,得到 $f'(x)=3x^2-2x-1$。
步骤 2:求二阶导数
对一阶导数 $f'(x)=3x^2-2x-1$ 求二阶导数,得到 $f''(x)=6x-2$。
步骤 3:确定凹凸区间
令二阶导数 $f''(x)=6x-2$ 大于0,得到 $x>\frac{1}{3}$,此时函数为凹的;令二阶导数 $f''(x)=6x-2$ 小于0,得到 $x<\frac{1}{3}$,此时函数为凸的。
步骤 4:确定拐点
令二阶导数 $f''(x)=6x-2$ 等于0,得到 $x=\frac{1}{3}$,此时函数的凹凸性发生变化,即拐点的横坐标为 $\frac{1}{3}$。将 $x=\frac{1}{3}$ 代入原函数 $f(x)={x}^{3}-{x}^{2}-x+1$,得到 $f(\frac{1}{3})=\frac{1}{27}-\frac{1}{9}-\frac{1}{3}+1=\frac{16}{27}$,即拐点的纵坐标为 $\frac{16}{27}$。
对函数 $f(x)={x}^{3}-{x}^{2}-x+1$ 求一阶导数,得到 $f'(x)=3x^2-2x-1$。
步骤 2:求二阶导数
对一阶导数 $f'(x)=3x^2-2x-1$ 求二阶导数,得到 $f''(x)=6x-2$。
步骤 3:确定凹凸区间
令二阶导数 $f''(x)=6x-2$ 大于0,得到 $x>\frac{1}{3}$,此时函数为凹的;令二阶导数 $f''(x)=6x-2$ 小于0,得到 $x<\frac{1}{3}$,此时函数为凸的。
步骤 4:确定拐点
令二阶导数 $f''(x)=6x-2$ 等于0,得到 $x=\frac{1}{3}$,此时函数的凹凸性发生变化,即拐点的横坐标为 $\frac{1}{3}$。将 $x=\frac{1}{3}$ 代入原函数 $f(x)={x}^{3}-{x}^{2}-x+1$,得到 $f(\frac{1}{3})=\frac{1}{27}-\frac{1}{9}-\frac{1}{3}+1=\frac{16}{27}$,即拐点的纵坐标为 $\frac{16}{27}$。