1.求下列极限:-|||-(1) lim _(xarrow 0)dfrac ({e)^xcos x+5}(1+{x)^2+ln (1-x)} =-|||-(3) lim _(xarrow {0)^-}(sqrt (dfrac {1)(x)+sqrt (dfrac {1)(x)+sqrt (dfrac {1)(x)}}}-sqrt (dfrac {1)(x)-sqrt (dfrac {1)(x)+sqrt (dfrac {1)(x)}})}-|||-√(1/x)-√(1/(x-√(x+√x)/-|||-(4) lim _(xarrow +infty )dfrac (sqrt {x+sqrt {x+sqrt {x)}}}(sqrt {x+1)}-|||-(2) lim _(xarrow +infty )(sqrt (x+sqrt {x+sqrt {x)}}-sqrt (x)) ;-|||-;(5) lim _(xarrow 0)((1+sin x))^cot x
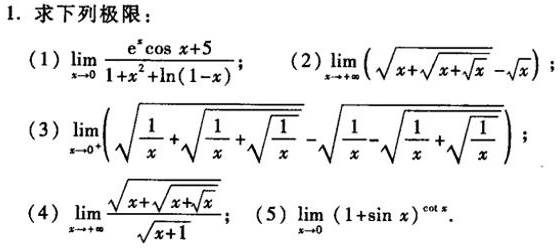
题目解答
答案
解析
题目1(1):$\lim _{x\rightarrow 0}\dfrac {{e}^{x}\cos x+5}{1+{x}^{2}+\ln (1-x)}$
考察知识:极限的代入法(连续函数的极限等于函数值)。
解题思路:当$x\rightarrow0$时,分子分母中的函数均连续,直接代入$x=0$计算:
- 分子:$e^0\cos0 + 5 = 1\cdot1 + 5 = 6$
- 分母:$1 + 0^2 + \ln(1-0) = 1 + 0 + 0 = 1$
结果:$\frac{6}{1}=6$。
题目1(2):$\lim _{x\rightarrow +\infty }(\sqrt {x+\sqrt {x+\sqrt {x}}}-\sqrt {x})$
考察知识:无穷大根式的极限(分子有理化)。
解题思路:根号差形式通过分子有理化化简:
$\begin{align*}&\sqrt{x+\sqrt{x+\sqrt{x}}}-\sqrt{x}\\=&\frac{(\sqrt{x+\sqrt{x+\sqrt{x}}}-\sqrt{x})(\sqrt{x+\sqrt{x+\sqrt{x}}}+\sqrt{x})}{\sqrtsqrt{x+\sqrt{x+\sqrt{x}}}+\sqrt{x}}\\=&\frac{(x+\sqrt{x+\sqrt{x}})-x)}{\sqrt{x+\sqrt{x+\sqrt{x}}}+\sqrt{x}}=\frac{\sqrt{x+\sqrt{x}}}{\sqrt{x+\sqrt{x+\sqrt{x}}}+\sqrt{x}}\end{align*}$
分子分母同除以$\sqrt{x}$:
$\frac{\sqrt{1+\sqrt{x}}}{\sqrt{1+\sqrt[4]{x}+\sqrt[8]{x}}+1}\rightarrow\frac{1}{1+1}=\frac{1}{2}$
结果:$\frac{1}{2}$。
题目1(3):$\lim_{x→0⁻}(√(1/x + √(1/x + √(1/x))) - √(1/x - √(1/x + √(1/x))))
考察知识:复合根式的化简(换元法)。
解题思路:设$t=\frac{1}{x}$($t→+∞$),则:
$\text{原式}=\sqrt{t+\sqrt{t+\sqrt{t^{1/2}}}}-\sqrt{t-\sqrt{t+\sqrt{t}}}$
分子有理化:
$=\frac{(t+\sqrt{t+\sqrt{t}})-(t-\sqrt{t+\sqrt{t}})}{\sqrt{t+\sqrt{t+\sqrt{t}}}+\sqrt{t-\sqrt{t+\sqrt{t}}}$
分子$=2\sqrt{t+\sqrt{t}}$,分母$=2\sqrt{t}+o(\sqrt{t})$,同除以$\sqrt{t}$得:
$\frac{2\sqrt{1+\frac{1}{\sqrt{t}}}}{2(1+o(1))}\rightarrow1$
结果:$1$。
题目1(4):$\lim _{x\rightarrow +\infty }\dfrac {\sqrt {x+\sqrt {x+\sqrt {x}}}}{\sqrt {x+1}}$
考察知识:无穷大根式的极限(同除最高次项)。
解题思路:分子分母同除以$\sqrt{x}$:
$\frac{\sqrt{1+\sqrt{\frac{1}{x}}+\sqrt{\frac{1}{x^3}}}}{\sqrt{1+\frac{1x}}\rightarrow\frac{\sqrt{1+0+0}}{\sqrt{1+0}}=1$
结果:$1$。
题目1(5):$\lim _{x\rightarrow 0}{(1+\sin x)}^{\cot x}$
考察知识:重要极限$(1+u)^{\frac{1}{u}}\rightarrow e$($u→0$)。
解题思路:$\cot x=\frac{\cos x}{\sin x}$,设$u=\sin x$($u→0$),则:
$(1+u)^{\frac{\cos x}{u}}=\left[(1+u)^{\frac{1}{u}}\right]^{\cos x}\rightarrow e^1=e$
结果:$e$。