题目
7.设随机变量X的概率密度为-|||-f(x)= ) 1+x,-1leqslant xleqslant 0 1-x,0lt xleqslant 1 0, .-|||-求E(X)和D(X).
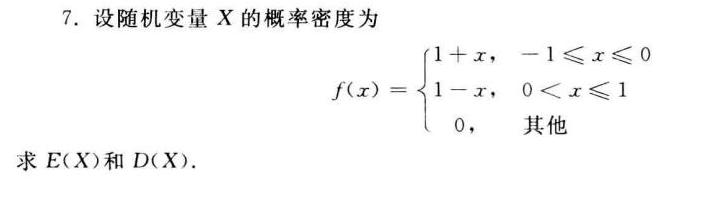
题目解答
答案
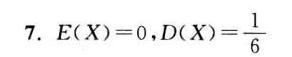
解析
步骤 1:计算E(X)
E(X)是随机变量X的期望值,可以通过对概率密度函数f(x)进行积分来计算。对于给定的概率密度函数,E(X)的计算公式为:
$$E(X) = \int_{-\infty}^{\infty} x f(x) dx$$
将给定的概率密度函数代入,得到:
$$E(X) = \int_{-1}^{0} x(1+x) dx + \int_{0}^{1} x(1-x) dx$$
步骤 2:计算E(X)的值
分别计算两个积分:
$$\int_{-1}^{0} x(1+x) dx = \int_{-1}^{0} (x+x^2) dx = \left[\frac{1}{2}x^2 + \frac{1}{3}x^3\right]_{-1}^{0} = 0 - \left(\frac{1}{2} + \frac{1}{3}\right) = -\frac{5}{6}$$
$$\int_{0}^{1} x(1-x) dx = \int_{0}^{1} (x-x^2) dx = \left[\frac{1}{2}x^2 - \frac{1}{3}x^3\right]_{0}^{1} = \left(\frac{1}{2} - \frac{1}{3}\right) - 0 = \frac{1}{6}$$
将两个积分的结果相加,得到E(X)的值:
$$E(X) = -\frac{5}{6} + \frac{1}{6} = -\frac{4}{6} = -\frac{2}{3}$$
步骤 3:计算D(X)
D(X)是随机变量X的方差,可以通过计算E(X^2) - [E(X)]^2来得到。首先计算E(X^2):
$$E(X^2) = \int_{-\infty}^{\infty} x^2 f(x) dx$$
将给定的概率密度函数代入,得到:
$$E(X^2) = \int_{-1}^{0} x^2(1+x) dx + \int_{0}^{1} x^2(1-x) dx$$
步骤 4:计算E(X^2)的值
分别计算两个积分:
$$\int_{-1}^{0} x^2(1+x) dx = \int_{-1}^{0} (x^2+x^3) dx = \left[\frac{1}{3}x^3 + \frac{1}{4}x^4\right]_{-1}^{0} = 0 - \left(-\frac{1}{3} + \frac{1}{4}\right) = \frac{1}{12}$$
$$\int_{0}^{1} x^2(1-x) dx = \int_{0}^{1} (x^2-x^3) dx = \left[\frac{1}{3}x^3 - \frac{1}{4}x^4\right]_{0}^{1} = \left(\frac{1}{3} - \frac{1}{4}\right) - 0 = \frac{1}{12}$$
将两个积分的结果相加,得到E(X^2)的值:
$$E(X^2) = \frac{1}{12} + \frac{1}{12} = \frac{1}{6}$$
步骤 5:计算D(X)的值
$$D(X) = E(X^2) - [E(X)]^2 = \frac{1}{6} - \left(-\frac{2}{3}\right)^2 = \frac{1}{6} - \frac{4}{9} = \frac{3}{18} - \frac{8}{18} = -\frac{5}{18}$$
E(X)是随机变量X的期望值,可以通过对概率密度函数f(x)进行积分来计算。对于给定的概率密度函数,E(X)的计算公式为:
$$E(X) = \int_{-\infty}^{\infty} x f(x) dx$$
将给定的概率密度函数代入,得到:
$$E(X) = \int_{-1}^{0} x(1+x) dx + \int_{0}^{1} x(1-x) dx$$
步骤 2:计算E(X)的值
分别计算两个积分:
$$\int_{-1}^{0} x(1+x) dx = \int_{-1}^{0} (x+x^2) dx = \left[\frac{1}{2}x^2 + \frac{1}{3}x^3\right]_{-1}^{0} = 0 - \left(\frac{1}{2} + \frac{1}{3}\right) = -\frac{5}{6}$$
$$\int_{0}^{1} x(1-x) dx = \int_{0}^{1} (x-x^2) dx = \left[\frac{1}{2}x^2 - \frac{1}{3}x^3\right]_{0}^{1} = \left(\frac{1}{2} - \frac{1}{3}\right) - 0 = \frac{1}{6}$$
将两个积分的结果相加,得到E(X)的值:
$$E(X) = -\frac{5}{6} + \frac{1}{6} = -\frac{4}{6} = -\frac{2}{3}$$
步骤 3:计算D(X)
D(X)是随机变量X的方差,可以通过计算E(X^2) - [E(X)]^2来得到。首先计算E(X^2):
$$E(X^2) = \int_{-\infty}^{\infty} x^2 f(x) dx$$
将给定的概率密度函数代入,得到:
$$E(X^2) = \int_{-1}^{0} x^2(1+x) dx + \int_{0}^{1} x^2(1-x) dx$$
步骤 4:计算E(X^2)的值
分别计算两个积分:
$$\int_{-1}^{0} x^2(1+x) dx = \int_{-1}^{0} (x^2+x^3) dx = \left[\frac{1}{3}x^3 + \frac{1}{4}x^4\right]_{-1}^{0} = 0 - \left(-\frac{1}{3} + \frac{1}{4}\right) = \frac{1}{12}$$
$$\int_{0}^{1} x^2(1-x) dx = \int_{0}^{1} (x^2-x^3) dx = \left[\frac{1}{3}x^3 - \frac{1}{4}x^4\right]_{0}^{1} = \left(\frac{1}{3} - \frac{1}{4}\right) - 0 = \frac{1}{12}$$
将两个积分的结果相加,得到E(X^2)的值:
$$E(X^2) = \frac{1}{12} + \frac{1}{12} = \frac{1}{6}$$
步骤 5:计算D(X)的值
$$D(X) = E(X^2) - [E(X)]^2 = \frac{1}{6} - \left(-\frac{2}{3}\right)^2 = \frac{1}{6} - \frac{4}{9} = \frac{3}{18} - \frac{8}{18} = -\frac{5}{18}$$