题目
6.函数 =xcos x 在 (-infty ,+infty ) 内是否有界?这个函数是否为 arrow +infty 时的无穷大?为什-|||-么?-|||-7.证明:函数 =dfrac (1)(x)sin dfrac (1)(x) 在区间(0,1]内无界,但这函数不是x→0^+时的无穷大.-|||-8.求函数 (x)=dfrac (4)(2-{x)^2} 的图形的渐近线.

题目解答
答案
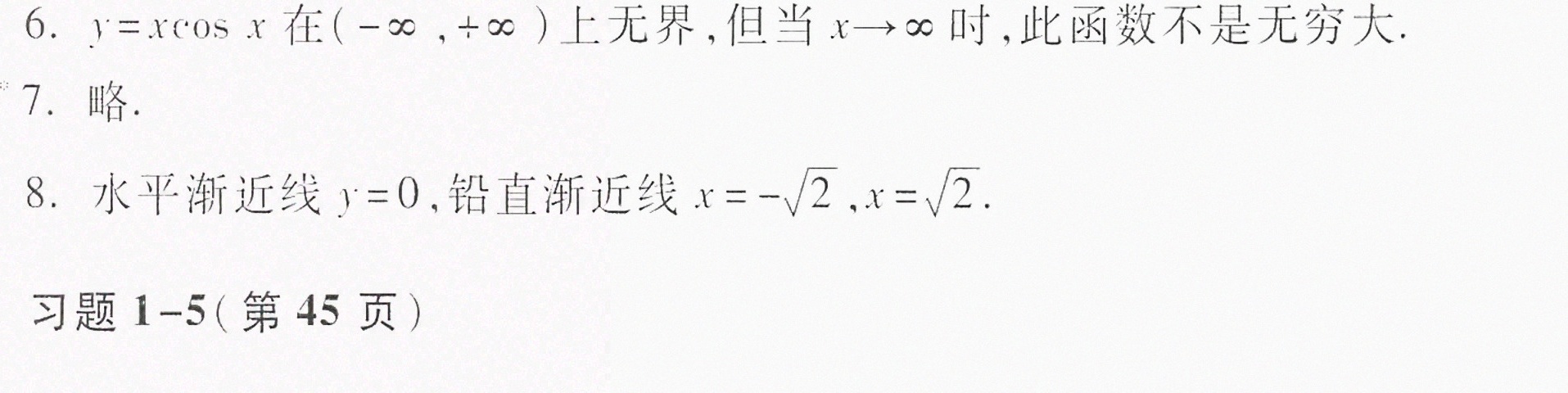
解析
6. 函数 $y=x\cos x$ 的有界性和无穷大性
本题考查有界函数和无穷大的概念。关键点在于:
- 有界性:虽然 $\cos x$ 有界,但乘以无界变量 $x$ 后,整体可能无界。
- 无穷大:当 $x \to +\infty$ 时,$\cos x$ 的周期性振荡会导致函数值无法稳定趋向无穷大。
8. 函数渐近线的求解
本题考查水平渐近线和垂直渐近线的求法:
- 水平渐近线:计算 $\lim_{x \to \pm\infty} f(x)$。
- 垂直渐近线:找出使分母为零的 $x$ 值。
6. 函数 $y=x\cos x$ 的分析
是否有界?
关键思路:构造特定点使函数值无界。
取 $x = 2k\pi$($k$ 为正整数),此时 $\cos x = 1$,函数值为 $y = x \cdot 1 = x$。当 $k \to +\infty$ 时,$y \to +\infty$,因此函数在 $(-\infty, +\infty)$ 上无界。
是否为无穷大?
关键思路:$\cos x$ 的周期性导致振荡。
当 $x \to +\infty$ 时,$\cos x$ 在 $[-1, 1]$ 间无限次振荡,使得 $y = x\cos x$ 在正负区间交替变化,无法趋向正无穷或负无穷。因此,不是无穷大。
8. 函数 $f(x) = \dfrac{4}{2 - x^2}$ 的渐近线
水平渐近线
计算 $\lim_{x \to \pm\infty} \dfrac{4}{2 - x^2}$:
分母 $2 - x^2 \approx -x^2$,故极限为 $\lim_{x \to \pm\infty} \dfrac{4}{-x^2} = 0$,因此水平渐近线为 $y = 0$。
铅直渐近线
解方程 $2 - x^2 = 0$,得 $x = \pm\sqrt{2}$。当 $x \to \pm\sqrt{2}$ 时,分母趋近于 $0$,函数值趋向无穷大,因此铅直渐近线为 $x = \pm\sqrt{2}$。