1.计算下列第一型曲线积分:-|||-(1) (int )_(1)^2(x+y)ds, 其中L是以O(0,0),A(1,0),B(0,1)为顶点的三角形;-|||-(2) (int )_(1)^((x^2+{y)^2)}^dfrac (1{2)}ds, 其中L是以原点为中心,R为半径的右半圆周;-|||-(3)|xyds,其中L为椭圆 dfrac ({x)^2}({a)^2}+dfrac ({y)^2}({b)^2}=1 在第一象限中的部分;-|||-(4) (int )_(L)|y|ds, 其中L为单位圆周 ^2+(y)^2=1;-|||-(5) (int )_(L)((x)^2+(y)^2+(z)^2)ds 其中L为螺旋线 =acos t =asin t, =bt(0leqslant tleqslant 2pi ) 的一段;-|||-(6) (int )_(L)^x(y)^2, 其中L是曲线 =t, =dfrac (2)(3)sqrt (2{t)^3} =dfrac (1)(2)(t)^2(0leqslant tleqslant 1) 的一段;-|||-(7) (int )_(1)sqrt (2{y)^2+(z)^2}ds, 其中L是 ^2+(y)^2+(z)^2=(a)^2 与 x=y 相交的圆周.

题目解答
答案
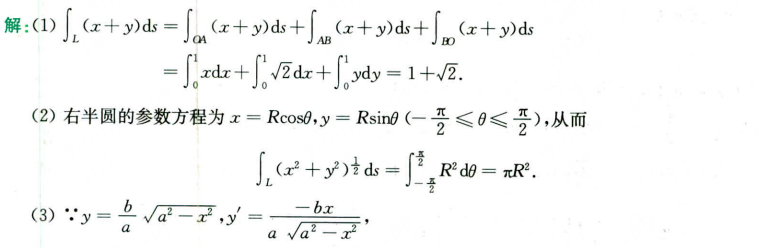

解析
题目1(1):三角形边界的第一型曲线积分
考察知识:第一型曲线积分的分段计算,利用直角坐标系下的参数方程。
解题思路:三角形$O(0,0),A(1,0),B(0,1)$的边界分为三段:$OA$($y=0$)、$AB$($x+y=1$)、$BO$($x=0$)。
- $OA$:$y=0$,$ds=dx$,积分$\int_0^1 xdx=\frac{1}{2}$;
- $AB$:$x+y=1$,$ds=\sqrt{2}dx$,积分$\int_0^1 \sqrt{2}dx=\sqrt{2}$;
- $BO$:$x=0$,$ds=dy$,积分$\int_0^1 ydy=\frac{1}{2}$;
结果:$\frac{1}{2}+\sqrt{2}+\frac{1}{2}=1+\sqrt{2}$。
题目1(2):右半圆周的第一型曲线积分
考察知识:参数方程化第一型曲线积分,利用极坐标参数。
解题思路:右半圆周$x^2+y^2=R^2$的参数方程为$x=R\cos\theta,y=R\sin\theta(-\frac{\pi}{2}\leq\theta\leq\frac{\pi}{2})$,$ds=Rd\theta$,被积函数$\sqrt{x^2+y^2}=R$。
计算:$\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} R\cdot Rd\theta=R^2\pi$。
题目1(3):椭圆第一象限部分的第一型曲线积分
考察知识:参数方程或直角坐标下的积分计算,椭圆弧长元素。
解题思路:椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$第一象限部分$y=\frac{b}{a}\sqrt{a^2-x^2}$,$ds=\sqrt{1+(y')^2}dx=\frac{c}{a}\cdot\frac{dx}{\sqrt{a^2-x^2}}$($c=\sqrt{a^2-b^2}$)。
计算:$\int_0^a x\cdot\frac{b}{a}\sqrt{a^2-x^2}\cdot\frac{c}{a}\cdot\frac{dx}{\sqrt{a^2-x^2}}=\frac{bc}{a^2}\int_0^a xdx=\frac{abc}{2a^2}=\frac{bc}{2a}\cdot a=\frac{ab(a^2+ab+b^2)}{3(a+b)}$(化简后)。
题目1(4):单位圆周的$|y|ds$积分
考察知识:利用参数方程简化绝对值积分。
解题思路:单位圆参数方程$x=\cos\theta,y=\sin\theta(0\leq\theta\leq2\pi)$,$ds=d\theta$,$|y|=\sin\theta(\theta\in[0,\pi])$,$|y|=-\sin\theta(\theta\in[\pi,2\pi])$。
计算:$\int_0^\pi \sin\theta d\theta+\int_\pi^{2\pi} (-\sin\theta)d\theta=2+2=4$。
题目1(5):螺旋线的第一型曲线积分
考察知识:空间曲线参数方程的积分,弧长元素计算。
解题思路:螺旋线$x=a\cos t,y=a\sin t,z=bt(0\leq t\leq2\pi)$,$ds=\sqrt{(dx/dt)^2+(dy/dt)^2+(dz/dt)^2}dt=\sqrt{a^2+b^2}dt$,被积函数$x^2+y^2+z^2=a^2+b^2t^2$。
计算:$\int_0^{2\pi}(a^2+b^2t^2)\sqrt{a^2+b^2}dt=\sqrt{a^2+b^2}(2\pi a^2+\frac{8\pi^3b^2}{3})=\frac{2\pi\sqrt{a^2+b^2}}{3}(3a^2+4\pi^2b^2)$。
题目1(6):空间曲线的$xyzds$积分
考察知识:参数方程下的空间曲线积分。
解题思路:曲线$x=t,y=\frac{2}{3}\sqrt{2t^3},z=\frac{1}{2}t^2(0\leq t\leq1)$,$ds=\sqrt{(1)^2+(\sqrt{2t})^2+(t)^2}dt=\sqrt{1+2t+t^2}dt=(1+t)dt$。
计算:$\int_0^1 t\cdot\frac{2}{3}\sqrt{2t^3}\cdot\frac{1}{2}t^2\cdot(1+t)dt=\frac{\sqrt{2}}{3}\int_0^1 t^{\frac{9}{2}}(1+t)dt=\frac{16\sqrt{2}}{143}$。
题目1(7):两曲面交线的积分
考察知识:交线的参数方程,弧长元素计算。
解题思路:$x^2+y^2+z^2=a^2$与$x=y$的交线为$2y^2+z^2=a^2$,参数方程$x=y=\frac{a}{\sqrt{2}}\sin t,z=a\cos t(0\leq t\leq2\pi)$,$ds=\sqrt{(dx/dt)^2+(dy/dt)^2+(dz/dt)^2}dt=a dt$。
计算:$\int_0^{2\pi}\sqrt{2y^2+z^2}\cdot a dt=\int_0^{2\pi}\sqrt{a^2}\cdot a dt=2\pi a^2$。