题目
7.计算下列各行列式(Dn为n阶行列式):-|||-a 1-|||-(1)Dn= 其中对角线上元素都是a,未写出的元素都是0.-|||-1 a7.计算下列各行列式(Dn为n阶行列式):-|||-a 1-|||-(1)Dn= 其中对角线上元素都是a,未写出的元素都是0.-|||-1 a


题目解答
答案


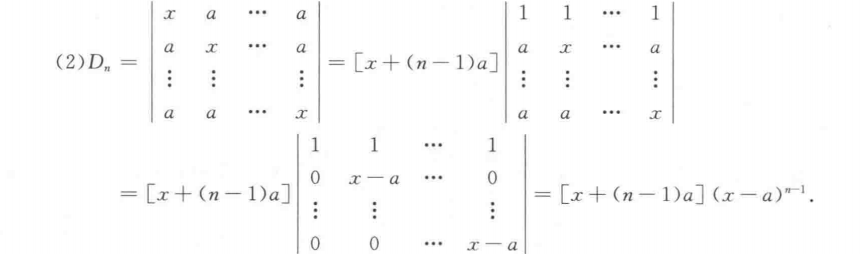
解析
考查要点:
本题主要考查特殊结构行列式的计算方法,包括对角线行列式、循环行列式的处理技巧,以及利用行列式的性质(如行变换、列变换、展开定理)进行化简的能力。
解题核心思路:
- 第一行列式:通过行变换将行列式转化为上三角或下三角形式,利用对角线元素的乘积求解。
- 第二行列式:通过列变换构造出公因子,利用行列式展开定理或范德蒙德行列式的变形求解。
破题关键点:
- 第一行列式的关键在于发现首尾行的特殊结构,通过行减操作生成非零元素,进而展开行列式。
- 第二行列式的关键在于统一非对角线元素,通过列加操作提取公因子,转化为已知形式的行列式。
第(1)题
行列式结构:
主对角线元素为$a$,第一行最后一个元素为$1$,最后一行第一个元素为$1$,其余元素为$0$。例如,$n=4$时:
$\begin{pmatrix}a & 1 & 0 & 0 \\1 & a & 0 & 0 \\0 & 0 & a & 1 \\1 & 0 & 0 & a\end{pmatrix}$
解题步骤:
- 行变换:将最后一行减去第一行,得到新最后一行为$(1-a, -1, 0, 0)$。
- 展开行列式:按最后一行展开,仅第一个元素$1-a$非零,对应子式为$(a^{n-2})$,其余元素展开后为$0$。
- 化简:最终结果为$(a^2 - 1)a^{n-2}$。
第(2)题
行列式结构:
主对角线元素为$x$,非对角线元素均为$a$。例如,$n=3$时:
$\begin{pmatrix}x & a & a \\a & x & a \\a & a & x\end{pmatrix}$
解题步骤:
- 列变换:将所有列加到第一列,第一列变为$(x + (n-1)a, a + (n-1)a, \dots, a + (n-1)a)$。
- 提取公因子:从第一列提取公因子$x + (n-1)a$,剩余行列式为$(x - a)^{n-1}$。
- 最终结果:$[x + (n-1)a](x - a)^{n-1}$。