题目
lim _(xarrow 4)dfrac (sqrt {2x+1)-3}(sqrt {x-2)-sqrt (2)}=.
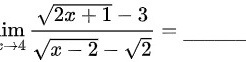 .
.
题目解答
答案
解:
∵ 该极限是 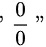 型极限
型极限
∴ 采用洛必达法则,得
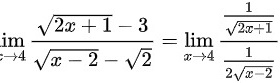
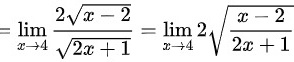
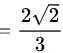
解析
考查要点:本题主要考查极限的计算方法,特别是0/0型不定式的处理技巧。需要掌握洛必达法则或分子分母有理化的解题思路。
解题核心思路:
当直接代入$x=4$导致分子分母均为0时,需通过变形消除不定式。
- 方法一:使用洛必达法则,对分子分母分别求导后求极限。
- 方法二:通过分子分母有理化,将分式化简为可直接代入的形式。
破题关键点:
- 识别极限类型为$\dfrac{0}{0}$型。
- 选择合适的方法(洛必达法则或有理化)简化表达式。
- 注意化简过程中代数运算的准确性。
方法一:洛必达法则
- 验证条件:当$x \rightarrow 4$时,分子$\sqrt{2x+1}-3 \rightarrow 0$,分母$\sqrt{x-2}-\sqrt{2} \rightarrow 0$,属于$\dfrac{0}{0}$型不定式,满足洛必达法则条件。
- 求导分子分母:
- 分子导数:$\dfrac{d}{dx}(\sqrt{2x+1}-3) = \dfrac{1}{\sqrt{2x+1}} \cdot 2 = \dfrac{1}{\sqrt{2x+1}}$
- 分母导数:$\dfrac{d}{dx}(\sqrt{x-2}-\sqrt{2}) = \dfrac{1}{2\sqrt{x-2}}$
- 应用洛必达法则:
$\lim _{x\rightarrow 4}\dfrac{\sqrt{2x+1}-3}{\sqrt{x-2}-\sqrt{2}} = \lim _{x\rightarrow 4} \dfrac{\dfrac{1}{\sqrt{2x+1}}}{\dfrac{1}{2\sqrt{x-2}}} = \lim _{x\rightarrow 4} \dfrac{2\sqrt{x-2}}{\sqrt{2x+1}}$ - 代入计算:
$\dfrac{2\sqrt{4-2}}{\sqrt{2 \cdot 4 +1}} = \dfrac{2\sqrt{2}}{3}$
方法二:分子分母有理化
- 分子有理化:
$(\sqrt{2x+1}-3)(\sqrt{2x+1}+3) = (2x+1) - 9 = 2x - 8 = 2(x-4)$ - 分母有理化:
$(\sqrt{x-2}-\sqrt{2})(\sqrt{x-2}+\sqrt{2}) = (x-2) - 2 = x - 4$ - 化简分式:
$\dfrac{2(x-4)}{x-4} \cdot \dfrac{\sqrt{x-2}+\sqrt{2}}{\sqrt{2x+1}+3} = 2 \cdot \dfrac{\sqrt{x-2}+\sqrt{2}}{\sqrt{2x+1}+3}$ - 代入计算:
$2 \cdot \dfrac{\sqrt{2}+\sqrt{2}}{3+3} = \dfrac{2 \cdot 2\sqrt{2}}{6} = \dfrac{2\sqrt{2}}{3}$