设 lt alt blt 1, 证明不等式 arctanb-arctana
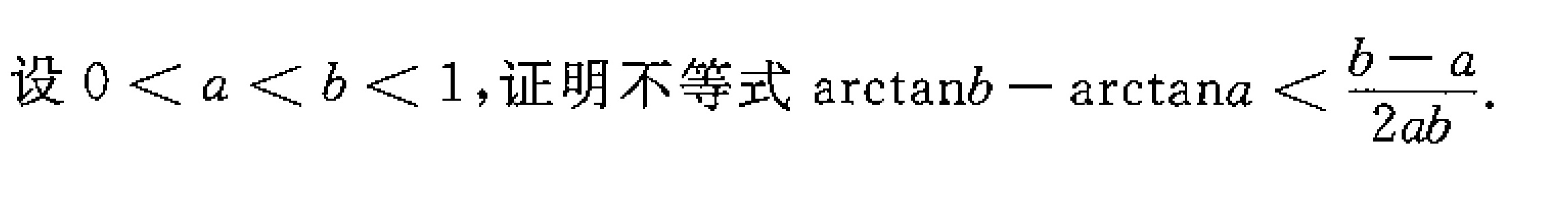
题目解答
答案
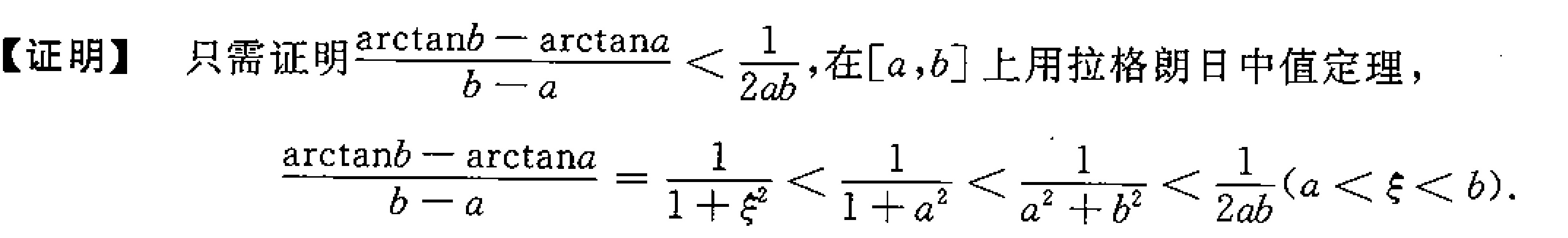
解析
考查要点:本题主要考查利用拉格朗日中值定理证明不等式,以及通过不等式链进行变形和放缩的能力。
解题核心思路:
- 构造函数:将不等式中的差商形式与导数联系起来,选择函数$f(x) = \arctan x$。
- 应用中值定理:在区间$[a, b]$上应用拉格朗日中值定理,将$\arctan b - \arctan a$表示为导数在某点的值乘以区间长度。
- 不等式变形:通过分析导数的表达式,结合$a < c < b$的条件,建立不等式链,最终完成证明。
破题关键点:
- 导数的单调性:$\frac{1}{1 + c^2}$随$c$增大而减小,利用$a < c < b$的范围进行放缩。
- 关键不等式:通过变形证明$2ab < 1 + c^2$,需结合$a < c$和均值不等式思想。
步骤1:应用拉格朗日中值定理
设$f(x) = \arctan x$,则$f'(x) = \frac{1}{1 + x^2}$。在区间$[a, b]$上,根据拉格朗日中值定理,存在$c \in (a, b)$,使得:
$\arctan b - \arctan a = f'(c)(b - a) = \frac{b - a}{1 + c^2}.$
步骤2:转化目标不等式
原不等式等价于:
$\frac{b - a}{1 + c^2} < \frac{b - a}{2ab}.$
两边同除以正数$b - a$,得:
$\frac{1}{1 + c^2} < \frac{1}{2ab}.$
进一步变形为:
$2ab < 1 + c^2.$
步骤3:分析$c$的范围
由于$c \in (a, b)$且$a < b < 1$,可知$c > a$,因此:
$c^2 > a^2 \quad \Rightarrow \quad 1 + c^2 > 1 + a^2.$
步骤4:建立关键不等式
需证明$1 + a^2 > 2ab$。变形得:
$1 + a^2 - 2ab = (a - b)^2 + 1 - b^2.$
因为$a < b < 1$,所以$(a - b)^2 > 0$且$1 - b^2 > 0$,故:
$1 + a^2 - 2ab > 0 \quad \Rightarrow \quad 1 + a^2 > 2ab.$
步骤5:综合不等式链
结合上述结果:
$1 + c^2 > 1 + a^2 > 2ab \quad \Rightarrow \quad 2ab < 1 + c^2.$
因此,原不等式成立。