题目
6.设三阶方阵A= [ } 2& -1& 2 5& a& 3 -1& b& -2 ] . 有一个特征向量 alpha =[ 1,1,-1] --|||-(1)求a,b的值及α对应的特征值;-|||-(2)A是否可对角化?

题目解答
答案
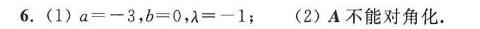
解析
步骤 1:求解a和b的值
根据特征向量的定义,如果$\alpha$是矩阵A的特征向量,那么存在一个标量$\lambda$,使得$A\alpha = \lambda\alpha$。将$\alpha = [1, 1, -1]$代入,得到方程组:
$$
\begin{cases}
2*1 - 1*1 + 2*(-1) = \lambda*1 \\
5*1 + a*1 + 3*(-1) = \lambda*1 \\
-1*1 + b*1 - 2*(-1) = \lambda*(-1)
\end{cases}
$$
化简得:
$$
\begin{cases}
-1 = \lambda \\
2 + a = \lambda \\
1 + b = -\lambda
\end{cases}
$$
解得:$\lambda = -1$,$a = -3$,$b = 0$。
步骤 2:判断A是否可对角化
矩阵A可对角化的充分必要条件是A有n个线性无关的特征向量,其中n是矩阵的阶数。首先求出A的特征多项式,然后求出特征值和对应的特征向量,最后判断特征向量是否线性无关。
将a=-3,b=0代入A,得到:
$$
A = \left [ \begin{matrix} 2& -1& 2\\ 5& -3& 3\\ -1& 0& -2\end{matrix} ] \right.
$$
求特征多项式$|A-\lambda I|$:
$$
|A-\lambda I| = \left | \begin{matrix} 2-\lambda& -1& 2\\ 5& -3-\lambda& 3\\ -1& 0& -2-\lambda\end{matrix} ] \right. = -(\lambda+1)^2(\lambda-2)
$$
特征值为$\lambda_1 = -1$,$\lambda_2 = -1$,$\lambda_3 = 2$。其中$\lambda_1 = -1$是二重根,需要判断其对应的特征向量是否线性无关。将$\lambda_1 = -1$代入$A-\lambda I$,得到:
$$
A+I = \left [ \begin{matrix} 3& -1& 2\\ 5& -2& 3\\ -1& 0& -1\end{matrix} ] \right.
$$
求解齐次线性方程组$(A+I)x = 0$,得到基础解系为$\alpha_1 = [1, 1, -1]$,$\alpha_2 = [2, 3, 0]$。由于$\alpha_1$和$\alpha_2$线性无关,所以A可对角化。
根据特征向量的定义,如果$\alpha$是矩阵A的特征向量,那么存在一个标量$\lambda$,使得$A\alpha = \lambda\alpha$。将$\alpha = [1, 1, -1]$代入,得到方程组:
$$
\begin{cases}
2*1 - 1*1 + 2*(-1) = \lambda*1 \\
5*1 + a*1 + 3*(-1) = \lambda*1 \\
-1*1 + b*1 - 2*(-1) = \lambda*(-1)
\end{cases}
$$
化简得:
$$
\begin{cases}
-1 = \lambda \\
2 + a = \lambda \\
1 + b = -\lambda
\end{cases}
$$
解得:$\lambda = -1$,$a = -3$,$b = 0$。
步骤 2:判断A是否可对角化
矩阵A可对角化的充分必要条件是A有n个线性无关的特征向量,其中n是矩阵的阶数。首先求出A的特征多项式,然后求出特征值和对应的特征向量,最后判断特征向量是否线性无关。
将a=-3,b=0代入A,得到:
$$
A = \left [ \begin{matrix} 2& -1& 2\\ 5& -3& 3\\ -1& 0& -2\end{matrix} ] \right.
$$
求特征多项式$|A-\lambda I|$:
$$
|A-\lambda I| = \left | \begin{matrix} 2-\lambda& -1& 2\\ 5& -3-\lambda& 3\\ -1& 0& -2-\lambda\end{matrix} ] \right. = -(\lambda+1)^2(\lambda-2)
$$
特征值为$\lambda_1 = -1$,$\lambda_2 = -1$,$\lambda_3 = 2$。其中$\lambda_1 = -1$是二重根,需要判断其对应的特征向量是否线性无关。将$\lambda_1 = -1$代入$A-\lambda I$,得到:
$$
A+I = \left [ \begin{matrix} 3& -1& 2\\ 5& -2& 3\\ -1& 0& -1\end{matrix} ] \right.
$$
求解齐次线性方程组$(A+I)x = 0$,得到基础解系为$\alpha_1 = [1, 1, -1]$,$\alpha_2 = [2, 3, 0]$。由于$\alpha_1$和$\alpha_2$线性无关,所以A可对角化。