题目
求下列极限:lim _(narrow infty )(1+dfrac (1)(2)+dfrac (1)(4)+... +dfrac (1)({2)^n}).
求下列极限:
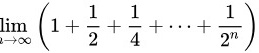 .
.
题目解答
答案
根据等比数列的求和公式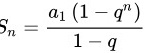 可得数列的和:(首项
可得数列的和:(首项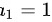 ,公比
,公比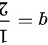 ,项数是
,项数是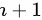 )
)
∴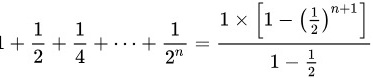
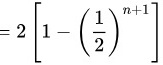 .
.
令 可得:
可得:
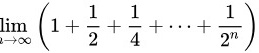
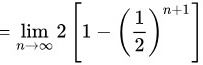
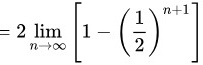
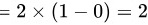 .
.
解析
考查要点:本题主要考查无穷等比数列求和的应用,需要掌握等比数列求和公式及其极限形式。
解题核心思路:
- 识别数列为首项为1,公比为$\dfrac{1}{2}$的等比数列。
- 判断公比绝对值是否小于1(本题中$\dfrac{1}{2} < 1$),从而确定可以使用无穷等比数列求和公式。
- 直接应用公式或通过有限项求和取极限求解。
破题关键点:
- 正确识别首项和公比,避免混淆项数与指数。
- 理解当$n \rightarrow \infty$时,$\left(\dfrac{1}{2}\right)^{n+1} \rightarrow 0$的数学依据。
步骤1:确认数列类型
题目中的数列为$1 + \dfrac{1}{2} + \dfrac{1}{4} + \cdots + \dfrac{1}{2^n}$,是首项$a_1 = 1$,公比$q = \dfrac{1}{2}$的等比数列。
步骤2:应用有限项求和公式
等比数列前$n+1$项和公式为:
$S_n = \dfrac{a_1(1 - q^{n+1})}{1 - q} = \dfrac{1 \cdot \left[1 - \left(\dfrac{1}{2}\right)^{n+1}\right]}{1 - \dfrac{1}{2}} = 2\left[1 - \left(\dfrac{1}{2}\right)^{n+1}\right]$
步骤3:取极限
当$n \rightarrow \infty$时,$\left(\dfrac{1}{2}\right)^{n+1} \rightarrow 0$,因此:
$\lim_{n \rightarrow \infty} S_n = \lim_{n \rightarrow \infty} 2\left[1 - \left(\dfrac{1}{2}\right)^{n+1}\right] = 2 \times (1 - 0) = 2$