题目
(2)已知齐次线性方程组 ) 3x+ky-z=0 4y+z=0 kx-5y-z=0 . 有非零解,则 ()-|||-A. k=0 B. k=1-|||-C. k=-1 或 k=-3 D. k=3
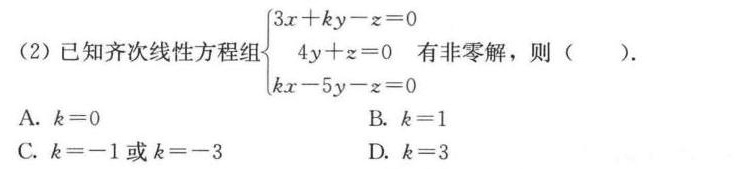
题目解答
答案
解析
考查要点:本题主要考查齐次线性方程组有非零解的条件,即系数矩阵的行列式为零。需要学生掌握行列式的计算方法,并能正确解二次方程。
解题核心思路:
- 构造系数矩阵:将方程组中的未知数系数按行排列成矩阵。
- 计算行列式:利用行列式的展开式或行变换求出行列式的表达式。
- 解方程:令行列式等于零,解出参数$k$的值。
破题关键点:
- 正确写出系数矩阵,注意每个方程中$x, y, z$的系数。
- 准确计算行列式,避免符号错误。
- 正确解二次方程,确保根的完整性。
步骤1:构造系数矩阵
方程组对应的系数矩阵为:
$\begin{pmatrix}3 & k & -1 \\0 & 4 & 1 \\k & -5 & -1\end{pmatrix}$
步骤2:计算行列式
行列式展开式为:
$\begin{aligned}\text{det} &= 3 \cdot (4 \cdot (-1) - 1 \cdot (-5)) - k \cdot (0 \cdot (-1) - 1 \cdot k) + (-1) \cdot (0 \cdot (-5) - 4 \cdot k) \\&= 3 \cdot (-4 + 5) - k \cdot (0 - k) + (-1) \cdot (0 - 4k) \\&= 3 \cdot 1 + k^2 + 4k \\&= k^2 + 4k + 3\end{aligned}$
步骤3:解行列式方程
令行列式等于零:
$k^2 + 4k + 3 = 0$
因式分解得:
$(k + 1)(k + 3) = 0$
解得:
$k = -1 \quad \text{或} \quad k = -3$