题目
17.设函数 (x)=lim _(narrow infty )dfrac ({x)^2n-1+a(x)^2+bx}({x)^2n+1} 是连续函数,求常数a,b.
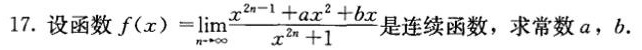
题目解答
答案
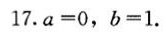
解析
步骤 1:分析极限表达式
首先,我们分析给定的极限表达式 $\lim _{n\rightarrow \infty }\dfrac {{x}^{2n-1}+a{x}^{2}+bx}{{x}^{2n}+1}$。当 $n$ 趋于无穷大时,$x^{2n}$ 项将主导分子和分母的值,除非 $x$ 的绝对值小于1。因此,我们需要分别考虑 $|x|>1$ 和 $|x|<1$ 的情况。
步骤 2:考虑 $|x|>1$ 的情况
当 $|x|>1$ 时,$x^{2n}$ 项将主导分子和分母的值。因此,我们可以将极限表达式简化为 $\lim _{n\rightarrow \infty }\dfrac {{x}^{2n-1}}{{x}^{2n}} = \lim _{n\rightarrow \infty }\dfrac {1}{x} = \dfrac {1}{x}$。这意味着当 $|x|>1$ 时,$f(x) = \dfrac {1}{x}$。
步骤 3:考虑 $|x|<1$ 的情况
当 $|x|<1$ 时,$x^{2n}$ 项将趋于0,因此极限表达式简化为 $\lim _{n\rightarrow \infty }\dfrac {a{x}^{2}+bx}{1} = a{x}^{2}+bx$。这意味着当 $|x|<1$ 时,$f(x) = a{x}^{2}+bx$。
步骤 4:考虑 $x=1$ 和 $x=-1$ 的情况
当 $x=1$ 或 $x=-1$ 时,$x^{2n}$ 项将始终为1,因此极限表达式简化为 $\lim _{n\rightarrow \infty }\dfrac {1+a+b}{2} = \dfrac {1+a+b}{2}$。这意味着当 $x=1$ 或 $x=-1$ 时,$f(x) = \dfrac {1+a+b}{2}$。
步骤 5:确保函数连续
为了使函数 $f(x)$ 在所有 $x$ 处连续,我们需要确保在 $x=1$ 和 $x=-1$ 处的极限值与函数值相等。因此,我们需要解方程 $\dfrac {1}{1} = \dfrac {1+a+b}{2}$ 和 $\dfrac {1}{-1} = \dfrac {1+a+b}{2}$。解这两个方程,我们得到 $a=0$ 和 $b=1$。
首先,我们分析给定的极限表达式 $\lim _{n\rightarrow \infty }\dfrac {{x}^{2n-1}+a{x}^{2}+bx}{{x}^{2n}+1}$。当 $n$ 趋于无穷大时,$x^{2n}$ 项将主导分子和分母的值,除非 $x$ 的绝对值小于1。因此,我们需要分别考虑 $|x|>1$ 和 $|x|<1$ 的情况。
步骤 2:考虑 $|x|>1$ 的情况
当 $|x|>1$ 时,$x^{2n}$ 项将主导分子和分母的值。因此,我们可以将极限表达式简化为 $\lim _{n\rightarrow \infty }\dfrac {{x}^{2n-1}}{{x}^{2n}} = \lim _{n\rightarrow \infty }\dfrac {1}{x} = \dfrac {1}{x}$。这意味着当 $|x|>1$ 时,$f(x) = \dfrac {1}{x}$。
步骤 3:考虑 $|x|<1$ 的情况
当 $|x|<1$ 时,$x^{2n}$ 项将趋于0,因此极限表达式简化为 $\lim _{n\rightarrow \infty }\dfrac {a{x}^{2}+bx}{1} = a{x}^{2}+bx$。这意味着当 $|x|<1$ 时,$f(x) = a{x}^{2}+bx$。
步骤 4:考虑 $x=1$ 和 $x=-1$ 的情况
当 $x=1$ 或 $x=-1$ 时,$x^{2n}$ 项将始终为1,因此极限表达式简化为 $\lim _{n\rightarrow \infty }\dfrac {1+a+b}{2} = \dfrac {1+a+b}{2}$。这意味着当 $x=1$ 或 $x=-1$ 时,$f(x) = \dfrac {1+a+b}{2}$。
步骤 5:确保函数连续
为了使函数 $f(x)$ 在所有 $x$ 处连续,我们需要确保在 $x=1$ 和 $x=-1$ 处的极限值与函数值相等。因此,我们需要解方程 $\dfrac {1}{1} = \dfrac {1+a+b}{2}$ 和 $\dfrac {1}{-1} = \dfrac {1+a+b}{2}$。解这两个方程,我们得到 $a=0$ 和 $b=1$。