题目
设两个相互独立的随机变量X,Y的分布律分别为X13Y24PX0.30.7PY0.60.4求随机变量Z = X + Y的分布律.
设两个相互独立的随机变量X,Y的分布律分别为
X
1
3
Y
2
4
PX
0.3
0.7
PY
0.6
0.4
求随机变量Z = X + Y的分布律.
题目解答
答案
解 随机变量Z = X + Y的可能取值为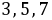 .
.
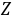 的分布律为
的分布律为
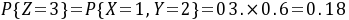 ,
,
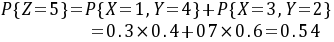 ,
,
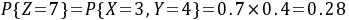 ,
,
或写为
Z | 3 | 5 | 7 |
PZ | 0.18 | 0.54 | 0.28 |
解析
考查要点:本题主要考查独立随机变量和的分布律的计算方法,需要理解独立性条件下联合概率的性质,并能正确列举所有可能的组合情况。
解题核心思路:
- 确定Z的可能取值:将X和Y的所有可能取值相加,得到Z的候选值。
- 合并重复值:若不同组合得到相同的和,则需合并对应概率。
- 计算概率:利用独立性,将各组合对应的联合概率相加。
破题关键点:
- 独立性应用:X与Y独立,故$P(X=x,Y=y)=P(X=x) \cdot P(Y=y)$。
- 穷举所有组合:确保所有可能的$(x,y)$组合都被考虑,避免遗漏。
步骤1:确定Z的可能取值
- X的取值为1、3,Y的取值为2、4。
- 所有可能的和为:
- $1+2=3$
- $1+4=5$
- $3+2=5$
- $3+4=7$
- 合并重复值,Z的可能取值为3、5、7。
步骤2:计算各取值的概率
Z=3
- 唯一组合:$X=1$且$Y=2$。
- 概率计算:
$P(Z=3) = P(X=1) \cdot P(Y=2) = 0.3 \times 0.6 = 0.18$
Z=5
- 两种组合:$X=1$且$Y=4$,或$X=3$且$Y=2$。
- 概率计算:
$P(Z=5) = P(X=1) \cdot P(Y=4) + P(X=3) \cdot P(Y=2) = 0.3 \times 0.4 + 0.7 \times 0.6 = 0.12 + 0.42 = 0.54$
Z=7
- 唯一组合:$X=3$且$Y=4$。
- 概率计算:
$P(Z=7) = P(X=3) \cdot P(Y=4) = 0.7 \times 0.4 = 0.28$
步骤3:验证概率和为1
$0.18 + 0.54 + 0.28 = 1.0$
验证通过,计算正确。