题目
[题目]计算定积分 (int )_(-4)^4sqrt (16-{x)^2}dx= __
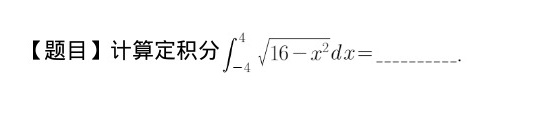
题目解答
答案

解析
考查要点:本题主要考查定积分的几何意义,即利用积分计算平面图形的面积。关键在于识别被积函数对应的几何图形。
解题核心思路:
被积函数为$\sqrt{16 - x^2}$,其平方后得到$x^2 + y^2 = 16$,表示半径为4的圆的上半部分。积分区间$[-4, 4]$对应圆的左右端点,因此积分结果等于半圆的面积。
破题关键点:
- 识别方程形式:将被积函数转化为圆的方程,明确图形为半圆。
- 应用面积公式:直接利用半圆面积公式$\frac{1}{2} \pi r^2$计算。
-
分析被积函数的几何意义
设$y = \sqrt{16 - x^2}$,两边平方得$x^2 + y^2 = 16$,表示以原点为圆心、半径为4的圆。由于$y \geq 0$,实际对应上半圆。 -
确定积分区间对应的图形范围
积分区间$x \in [-4, 4]$恰好覆盖上半圆的水平范围,因此积分$\int_{-4}^{4} \sqrt{16 - x^2} \, dx$表示上半圆的面积。 -
计算半圆面积
半径$r = 4$,面积为:
$\frac{1}{2} \times \pi \times 4^2 = 8\pi$