题目
在半径为的圆内画平行弦,如果这些弦与垂直与弦的直径的交点在该直径上的位置是等可能的,即交点在直径上一个区间内的可能性与此区间的长度成比例,求任意画弦的长度大于的概率。
在半径为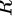 的圆内画平行弦,如果这些弦与垂直与弦的直径的交点在该直径上的位置是等可能的,即交点在直径上一个区间内的可能性与此区间的长度成比例,求任意画弦的长度大于
的圆内画平行弦,如果这些弦与垂直与弦的直径的交点在该直径上的位置是等可能的,即交点在直径上一个区间内的可能性与此区间的长度成比例,求任意画弦的长度大于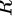 的概率。
的概率。
题目解答
答案
由题设可知这个概率可由几何方法确定。记弦的中点与圆心的距离为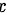 ,则样本空间为
,则样本空间为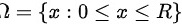 ,其长度为
,其长度为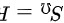 。由圆的性质可知时间
。由圆的性质可知时间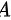 为“弦的长度大于 R ”可表示为
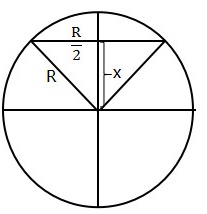
为“弦的长度大于 R ”可表示为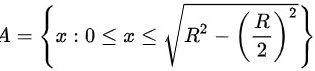 (如图),其长度为
(如图),其长度为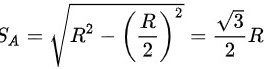
于是所求概率为
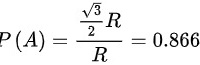
解析
考查要点:本题属于几何概率问题,核心在于理解均匀分布在几何模型中的应用,以及如何将弦长条件转化为几何量的限制范围。
解题思路:
- 确定样本空间:题目中交点在直径上的位置是等可能的,因此样本空间是直径上的一段区间,长度为$R$。
- 建立弦长与中点位置的关系:利用圆的几何性质,弦长$L$与中点到圆心的距离$x$满足$L = 2\sqrt{R^2 - x^2}$。
- 转化条件:将“弦长$> R$”转化为$x$的取值范围,计算满足条件的区间长度。
- 计算概率:用满足条件的区间长度除以总样本空间长度。
破题关键:正确建立弦长与中点位置的关系,并将不等式条件转化为$x$的范围。
步骤1:建立弦长与中点位置的关系
设弦的中点到圆心的距离为$x$,则弦长$L = 2\sqrt{R^2 - x^2}$。
步骤2:转化弦长条件
要求$L > R$,即:
$2\sqrt{R^2 - x^2} > R$
两边平方得:
$4(R^2 - x^2) > R^2 \implies 3R^2 > 4x^2 \implies x^2 < \frac{3}{4}R^2$
因此,$x$的取值范围为:
$0 \leq x \leq \frac{\sqrt{3}}{2}R$
步骤3:计算概率
- 总样本空间长度:$0 \leq x \leq R$,长度为$R$。
- 满足条件的区间长度:$0 \leq x \leq \frac{\sqrt{3}}{2}R$,长度为$\frac{\sqrt{3}}{2}R$。
- 概率:
$P = \frac{\frac{\sqrt{3}}{2}R}{R} = \frac{\sqrt{3}}{2} \approx 0.866$