题目
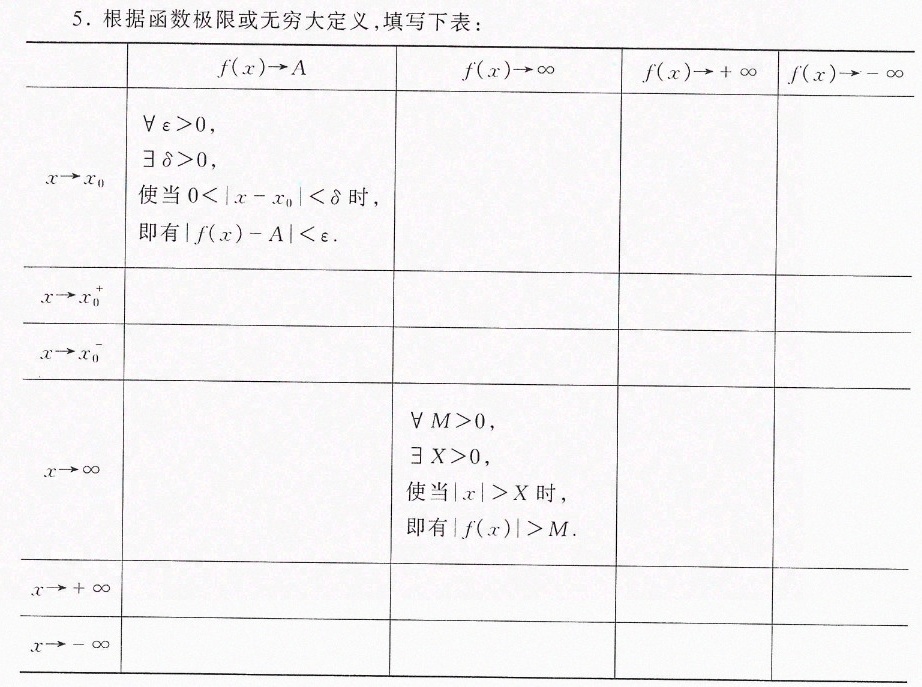
5.根据函数极限或无穷大定义,填写下表:-|||-(x)arrow A (x)arrow infty (x)arrow +infty (x)arrow -infty -|||-forall egt 0,-|||-gt 0,-|||-x→x0 使当 lt |x-(x)_(0)|lt 8 时,-|||-即有 |f(x)-A|lt e.-|||-arrow (x)_(0)+-|||-arrow (x)_(0)-|||-forall Mgt 0,-|||-gt 0,-|||-x→∞-|||-使当 |x|gt x 时,-|||-即有 |f(x)|gt M.-|||-arrow +infty -|||-arrow -infty
题目解答
答案
解析
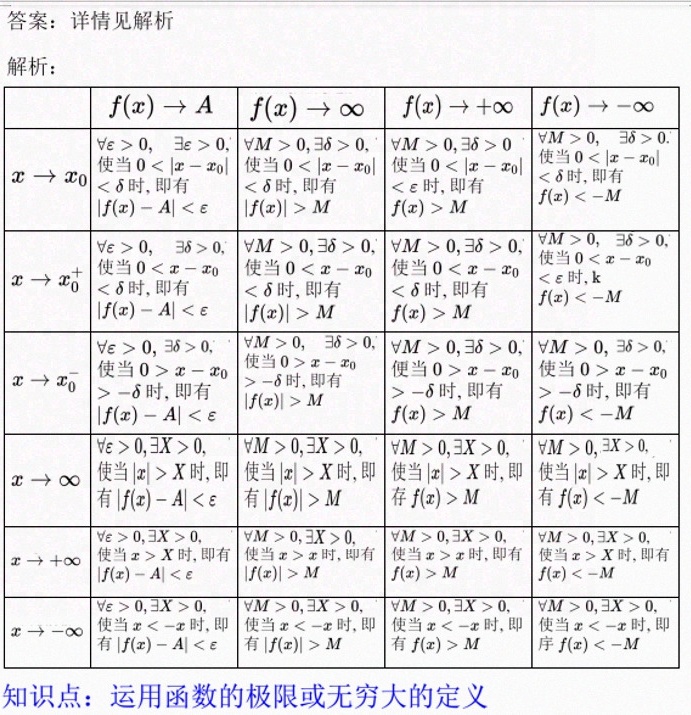
本题考查函数极限与无穷大定义的对应关系,需要根据不同的极限形式(如$f(x)\rightarrow A$、$f(x)\rightarrow \infty$等)和自变量的变化趋势(如$x\rightarrow x_0$、$x\rightarrow +\infty$等),填写对应的条件和结论。解题核心在于:
- 明确极限类型:区分函数趋向有限值、无穷大、正无穷、负无穷;
- 匹配定义结构:根据极限类型,选择对应的定义条件(如$\forall \varepsilon>0$或$\forall M>0$)和结论(如$|f(x)-A|<\varepsilon$或$f(x)>M$);
- 注意自变量趋势:区分$x\rightarrow x_0$时的邻域控制(用$\delta$)和$x\rightarrow \infty$时的远离原点控制(用$X$)。
表格填写逻辑
-
$f(x)\rightarrow A$:
- 条件:$\forall \varepsilon>0$,$\exists \delta>0$;
- 结论:$|f(x)-A|<\varepsilon$;
- 自变量趋势:
- $x\rightarrow x_0$时,$0<|x-x_0|<\delta$;
- $x\rightarrow \infty$时,$|x|>X$。
-
$f(x)\rightarrow \infty$:
- 条件:$\forall M>0$,$\exists \delta>0$(或$X>0$);
- 结论:$|f(x)|>M$;
- 自变量趋势同上。
-
$f(x)\rightarrow +\infty$:
- 结论:$f(x)>M$;
- 其余同$f(x)\rightarrow \infty$。
-
$f(x)\rightarrow -\infty$:
- 结论:$f(x)<-M$;
- 其余同$f(x)\rightarrow \infty$。
易错点
- 混淆$\varepsilon$与$M$:$f(x)\rightarrow A$用$\varepsilon$,无穷大用$M$;
- 符号方向:$+\infty$需$f(x)>M$,$-\infty$需$f(x)<-M$;
- 自变量控制:$x\rightarrow x_0$用$\delta$,$x\rightarrow \infty$用$X$。