题目
设一个袋中装有3个黑球,7个白球,现将球随机地一个个摸出,则第k次摸出黑球的概率是()(https:/img.zuoyebang.cc/zyb_9d7357ceae4904ef8e172e6617bb3b46.jpgleqslant kleqslant 10). A https:/img.zuoyebang.cc/zyb_49faa650c826dcd3cc546a2c70cc7539.jpgleqslant kleqslant 10;B https:/img.zuoyebang.cc/zyb_c618de3e84abda4e15b3e4b464b7ea6c.jpgleqslant kleqslant 10;C https:/img.zuoyebang.cc/zyb_af2e072c84b98e14945a9eecb3427b4a.jpgleqslant kleqslant 10;D https:/img.zuoyebang.cc/zyb_017ef8adf025d8b90ed4768b79d797a4.jpgleqslant kleqslant 10.
设一个袋中装有3个黑球,7个白球,现将球随机地一个个摸出,则第k次摸出黑球的概率是()
(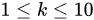 ).
).
A 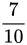 ;
;
B 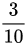 ;
;
C 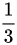 ;
;
D 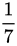 .
.
题目解答
答案
1. 分析问题:
因为是将球随机一个个摸出,所以每次摸球时袋中的球总数是相同的。
袋中一共有3个黑球和7个白球,总球数为3 + 7 = 10个。
2. 计算概率:
第k次摸出黑球的概率就等于黑球的个数除以总球数,即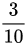 。
。
综上,答案是 B 选项。
解析
关键思路:本题考察等概率事件的理解。由于每次摸球是随机的,且所有球被摸出的可能性在各次位置上是对称的,因此第k次摸到黑球的概率等于黑球总数占总球数的比例,与k的具体位置无关。
核心概念:
- 对称性原理:每个球在任意位置被摸出的概率相同。
- 组合等价性:所有排列方式的可能性均等,因此黑球在第k次出现的概率仅由其数量比例决定。
步骤解析
- 总球数确定:袋中共有黑球3个,白球7个,总球数为 $3 + 7 = 10$ 个。
- 对称性分析:无论第k次摸球是第几次($1 \leq k \leq 10$),所有球在任意位置出现的可能性均等。
- 概率计算:
- 黑球共有3个,总共有10个球,因此黑球在第k次被摸出的概率为 $\dfrac{3}{10}$。
- 无需考虑顺序:因为所有排列方式的可能性相同,第k次的位置与其他位置的概率分布一致。
举例验证
假设袋中有1个黑球和1个白球,总球数2个:
- 第1次摸到黑球的概率为 $\dfrac{1}{2}$。
- 第2次摸到黑球的概率也为 $\dfrac{1}{2}$(若第1次摸到白球,则第2次必然摸到黑球)。
此例验证了对称性原理的正确性。