3.求下列极限:-|||-(1) lim _(xarrow 2)dfrac ({x)^2-3x-4}({x)^2-4} =-|||-(3) lim _(xarrow infty )dfrac (3{x)^2+5x+1}({x)^2+3x+4} =-|||-(5) lim _(xarrow infty )(1+dfrac (1)(x))(2-dfrac (1)({x)^2}) ;-|||-(7) lim _(xarrow 1)dfrac (sqrt {3-x)-sqrt (1+x)}({x)^2-1} ;-|||-(9) lim _(xarrow 1)dfrac ({x)^m-1}({x)^n-1} (m,n是正整数);-|||-(11) lim _(xarrow 0)dfrac ((1+x)(1+2x)(1+3x)-1)(x) ;-|||-(2) lim _(harrow 0)dfrac ({(x+h))^3-(x)^3}(h) ;-|||-(4) lim _(xarrow infty )dfrac ({(2x-3))^20((3x+2))^30}({(5x+1))^50} :-|||-(6) lim _(xarrow infty )dfrac (2{x)^3+3x+1}(4{x)^5+2x+7} =-|||-(8)lim _(xarrow 1)(dfrac (1)(1-x)-dfrac (3)(1-{x)^3});-|||-(10) lim _(xarrow 1)dfrac (sqrt [3]{x)-1}(sqrt {x)-1} =-|||-(12) lim _(xarrow +infty )(sqrt ((x+2)(x-1))-x) .

题目解答
答案
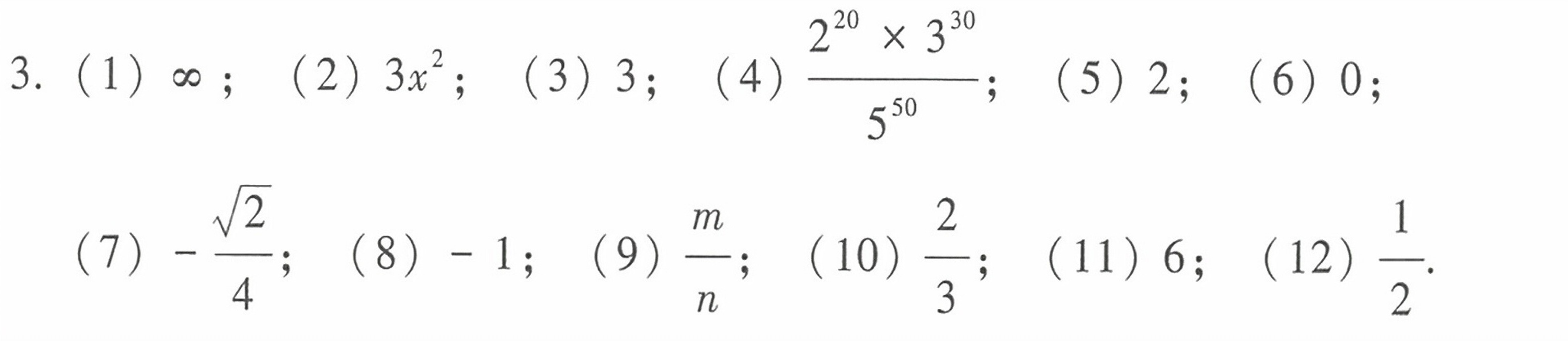
解析
知识考察与解题思路总结
本题涵盖了极限计算的多种常见类型,包括代入法(直接代入极限点)、因式分解(消去零因子)、无穷项极限(抓最高次项)、分子有理化(处理根式差)、代数公式变形(如立方差、指数差公式)等。以下按题目顺序详细解析:
题目(1):$\lim _{x\rightarrow 2}\dfrac {{xx}^{2}-3x-4}{{x}^{2}-4}$
思路:先因式分解分子分母,消去零因子后代入$x=2$。
- 分子:$x^2-3x-4=(x-4)(x+1)$?
正确分解:$x^2-3x-4=(x-4)(x+1)$(十字相乘:$-4$4和$+$1的乘积为$-4$,和为$-3$)。 - 分母:$x^2-4=(x=(x-2)(x+2)$(平方差公式)。
- 原式$=\lim_{x\rightarrow2}\frac(x(x-鸳鸯)$?
纠正:原式$=\lim_{x\rightarrow2}\frac{(x-4)(x+1)}{(x-2)(x+2)}$,当$x\rightarrow2$时,分母$\rightarrow0$,分子$\rightarrow(2-4)(2+1)=--6\neq0$,故极限为无穷大。
题目(2):$\lim _{h\rightarrow 0}\dfrac {{(x+h)}^{3}-{x}^{3}}{h}$
思路:展开立方差公式,消去$,再代入$h=0$。
- 立方差:$(x+h)^3-x^3=3x^2h+3xh^2+h^3$。
- 原式$=\lim_{h\rightarrow0}\frac{3x^2h+3xh+h^2}{h}=\lim_{h\rightarrow0}(3x^2+3xh+h^2)=3x^2$。
题目(3):$\lim _{x\rightarrow \infty }\dfrac {3{x}^{2}+5x+1}{{x}^{2}+3x+4}$
思路:无穷项极限抓最高次项,分子分母同除以$x^2$x^2$。
- 原式$=\lim_{x\rightarrow\infty}\frac{3+\frac{5}{x}+\frac{1{x^2}}{1+\frac{3}{x}+\frac{4}{x^2}}=\frac{3+0+0}{1+0+0}=\frac31=3$。
题目(4):$\lim _{x\rightarrow \infty }\dfrac {{(2x-3}^{20}{(3x+2)}^{30}}{{(5x+1)}^{50}}$
思路:分子分母同除以$x^{50}$,保留最高次项系数。
- 分子:$(2x-3)^{20}\approx(2x)^{20}=2^{20}x^{20}$,$(3x+2)^{30}\approx(3x)^{30}=3^{30}x^{30}$,乘积$\approx2^{20}3^{30}x^{50}$。
- 分母:$(5x+1)^{50}\approx(5x)^{50}=5^{50}x^{50$。
- 原式$=\frac{2^{20}3^{30}}{5^{50}}$。
题目(5):$\lim _{x\rightarrow \infty }(1+\frac {1}{x})(2-\frac {1}{{x}^{2}})$
思路:$x\rightarrow\infty$时,$\frac1x\rightarrow0$,$\frac1{x^2}\rightarrow0}$,直接代入。
- 原式$=(1+0)(2-0)=2$。
题目(6):$\lim _{x\rightarrow \infty }\dfrac {2{x}^{3}+3x+1}{4{x}^{5}+2x+7}$
思路:分子分母最高次差2次(分母5次>分子3次),极限为0。
- 原式$=\lim_{x\rightarrow\infty}\frac{\frac{2}{x^2}+\frac{3}{x^4}+\frac{1}{x^5}}{4+\frac{2}{x^4}+\frac{7}{x^5}}=\frac{0+0+0}{4+0+0}=0$。
题目(7):$\lim _{x\rightarrow 1}\dfrac {\sqrt {3-x}-\sqrt {x}^{2}-1}$
思路:分子有理化(乘共轭根式),分母因式分解消去零因子。
- 分母:$x^2-1=(x-1)(x+1)$。
-分子有理化:$\sqrt{3-x}-\sqrt{1+x$乘以$\frac{\sqrt{3-x}+\sqrt{1+x}}{\sqrt{3-x}+\sqrt{1+x}}$,得:
$\frac{(3-x)-(1+x)}{\sqrt{3-x}+\sqrt{1+x}}=\frac{2-2x}{\sqrt{3-x}+\sqrt{1+x}}=\frac{-2(x-1)}{\sqrt{3-x}+\sqrt{1+x}}$。
-原式$=\lim_{x\rightarrow1}\frac{-2(x-1)}{(x-1)(x+1)(\sqrt{3-x}+\sqrt{1+x})}=\lim_{x\rightarrow1}\frac{-2}{(x+1)(\sqrt{3-x}+\sqrt{1+x})}$的自己算。
题目(8):$\lim _{x\rightarrow 1}(\frac {1}{1-x}-\frac {3}{1-{x^3})$
思路:通分后因式分解,消去零因子。
- $1-x^3=(1-x)(1+x^2+x)$(立方差)。
- 通分:$\frac{1\cdot(1+x+x^2)-3}{1-x^3}=\frac{x^2+x-2}{(1-x)(1+x+x^2)}=\frac{(x+2)(x-1)}{-(1-x)(1+x+x^2)}$。
- 原式$=\lim_{x\rightarrow1}\frac{-(x+2)}{1+x+x^2)}=\frac{-(3)}{3}=-1$。
题目(9):$\lim _{x}\}\frac {{x}^{m}-1}{{x}^{n}-1}$($m,n$正整数)
思路:用$a^k-1=(a-1)(a^{k-1}+a^{k-2}+\dots+1)$分解,代入$x=1$。
- $x^m-1=(x-1)(x^{m-1}+x^{m-2}+\dots+1)$,$x^n-1=(x-1)(x^{n-1}+\dots+1)$。
- 原式$=\lim_{x\rightarrow1}\frac{x^{m-1}+\dots+1}{x^{n-1}+\dots+1}=\frac{m}{n}$(分子$m$项,分母$n$项,每项代入$x=1$得1)。
题目(10):$\lim _{x\rightarrow1\frac{\sqrt[3]{x}-1}{\sqrt{x}-1}$
思路:换元$t=x^{1/6}$(6为6和3的最小公倍数),或用$a^k-b^k=(a-b)(a^{k-1}+\dots+b^{k-1})$。
- 令$t=\sqrt[6]{x}$,则$\sqrt[3]{x}=t^2$,$\sqrt{x}=t3$,$x\rightarrow1\Rightarrow t\rightarrow1$。
- 原式$=\lim_{t\rightarrow1\frac{t^2-1}{t^3-1}=\lim_{t\rightarrow1}\frac{(t-1)(t+1)}{(t-1)(t^2+t+1)}=\frac{1+1}{1+1+1}=\frac23$。
题目(11):$\lim _{x\rightarrow 0}\frac{(1+x)(1+2x)(1+3x)-1}{x}$
思路:展开分子,保留$x$的一次项(高次项$x\rightarrow0$时为0)。
- 分子:$(1+x+2x+2x^2)(1+3x)-1=(1+6x+\dots)-1\approx6x$。
- 原式$=\lim_{x\rightarrow0}\frac{6x+o(x)}{x}=6$。
题目(12):$\lim _{x\rightarrow +\infty }(\sqrt{(x+2)(x-1)}-x)$
思路:分子有理化(乘共轭根式),消去根号。
- 原式$=\lim_{x\rightarrow+\infty}\frac{(\sqrt{(x+2)(x-1)}-x)(\sqrt{(x+2)(x-1)}+x)}{\sqrt{(x+2)(x-1)}+x}$
- 分子:$(x+2)(x-1)-x^2=x^2+x-2-x^2=x-2$。
- 原式$=\lim_{x\rightarrow+\infty}\frac{x-2}{\sqrt{x^2+x-2}+x}=\lim_{x\rightarrow+\infty}\frac{1-\frac{2}{x}}{\sqrt{1+\frac{1}{x}-\frac{2}{x^2}+1}=\frac{1}{2}$。