题目
计算 lim _(xarrow 0)dfrac (1)({x)^2}ln dfrac (sin x)(x) .
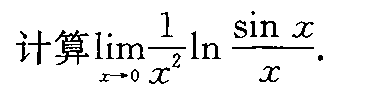
题目解答
答案
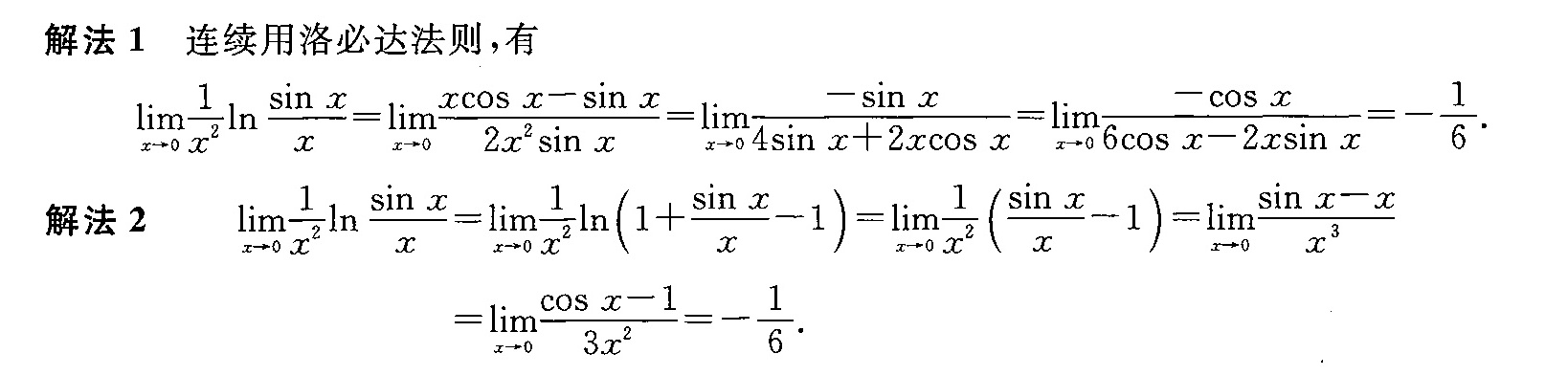
解析
本题考查利用洛必达法则求极限的知识点。解题思路是先判断极限的类型,若为$\frac{0}{0}$型或$\frac{\infty}{\infty}$型,则可使用洛必达法则对分子分母分别求导来计算极限。
- 首先判断极限类型:
当$x\rightarrow 0$时,$\sin x\sim x$,则$\lim _{x\rightarrow 0}\frac{\sin x}{x}=1$,那么$\lim _{x\rightarrow 0}\ln\frac{\sin x}{x}=\ln1 = 0$,同时$\lim _{x\rightarrow 0}x^{2}=0$,所以$\lim _{x\rightarrow 0}\frac{1}{x^{2}}\ln\frac{\sin x}{x}$是$\frac{0}{0}$型极限。 - 然后使用洛必达法则:
根据洛必达法则,若$\lim _{x\rightarrow a}\frac{f(x)}{g(x)}$是$\frac{0}{0}$型或$\frac{\infty}{\infty}$型,则$\lim _{x\rightarrow a}\frac{f(x)}{g(x)}=\lim _{x\rightarrow a}\frac{f^\prime(x)}{g^\prime(x)}$。
对$\frac{1}{x^{2}}\ln\frac{\sin x}{x}$的分子分母分别求导,先将$\frac{1}{x^{2}}\ln\frac{\sin x}{x}$变形为$\frac{\ln\sin x - \ln x}{x^{2}}$。- 求分子$\ln\sin x - \ln x$的导数:
根据求导公式$(\ln u)^\prime=\frac{u^\prime}{u}$,$(\sin x)^\prime = \cos x$,$(x)^\prime = 1$,可得$(\ln\sin x - \ln x)^\prime=\frac{\cos x}{\sin x}-\frac{1}{x}=\frac{x\cos x - \sin x}{x\sin x}$。 - 求分母$x^{2}$的导数:
根据求导公式$(x^n)^\prime = nx^{n - 1}$,可得$(x^{2})^\prime = 2x$。
则$\lim _{x\rightarrow 0}\frac{\ln\sin x - \ln x}{x^{2}}=\lim _{x\rightarrow 0}\frac{\frac{x\cos x - \sin x}{x\sin x}}{2x}=\lim _{x\rightarrow 0}\frac{x\cos x - \sin x}{2x^{2}\sin x}$。
当$x\rightarrow 0$时,$\sin x\sim x$,则$\lim _{x\rightarrow 0}\frac{x\cos x - \sin x}{2x^{2}\sin x}=\lim _{x\rightarrow 0}\frac{x\cos x - \sin x}{2x^{3}}$,此时该极限仍为$\frac{0}{0}$型。
- 求分子$\ln\sin x - \ln x$的导数:
- 再次使用洛必达法则:
- 求分子$x\cos x - \sin x$的导数:
根据求导公式$(uv)^\prime = u^\prime v + uv^\prime$,$(\cos x)^\prime = -\sin x$,$(\sin x)^\prime = \cos x$,可得$(x\cos x - \sin x)^\prime=\cos x - x\sin x - \cos x=-x\sin x$。 - 求分母$2x^{3}$的导数:
根据求导公式$(x^n)^\prime = nx^{n - 1}$,可得$(2x^{3})^\prime = 6x^{2}$。
则$\lim _{x\rightarrow 0}\frac{x\cos x - \sin x}{2x^{3}}=\lim _{x\rightarrow 0}\frac{-x\sin x}{6x^{2}}=\lim _{x\rightarrow 0}\frac{-\sin x}{6x}$。
当$x\rightarrow 0$时,$\lim _{x\rightarrow 0}\frac{\sin x}{x}=1$,所以$\lim _{x\rightarrow 0}\frac{-\sin x}{6x}=-\frac{1}{6}$。
- 求分子$x\cos x - \sin x$的导数: