1.21 求矢量 =(e)_(x)x+(e)_(y)(x)^2+(e)_(2)(y)^2z 沿xy平面上的一个边长为2的正方形-|||-回路的线积分,此正方形的两边分别与x轴和y轴相重合。再求 times A 对此回-|||-路所包围的曲面积分,验证斯托克斯定理。

题目解答
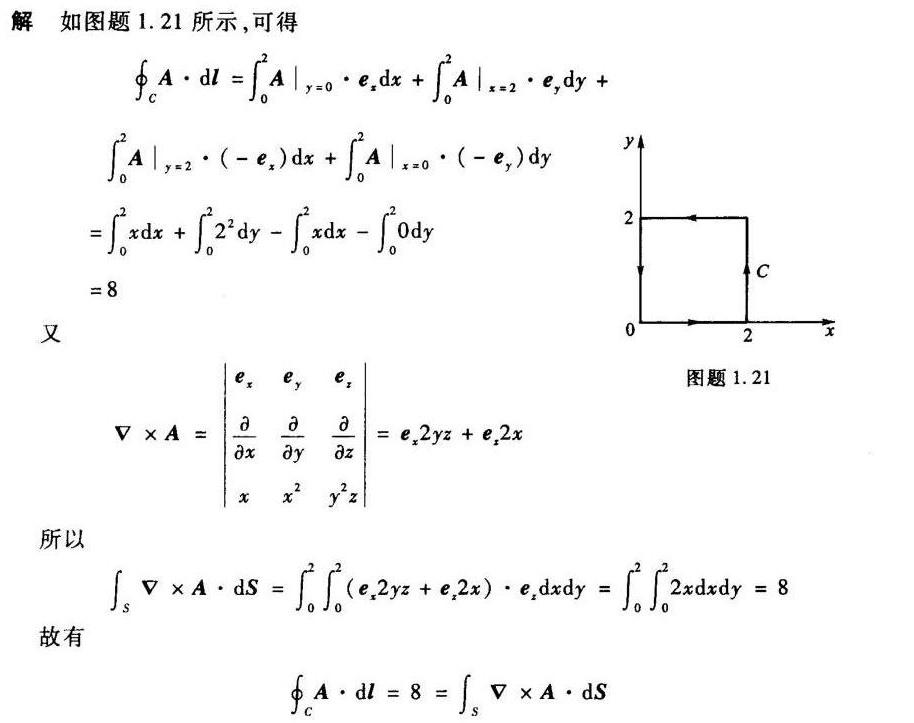
答案
解析
题目考察知识
本题主要考察斯托克斯定理的应用,需完成两个核心计算:矢量$A$沿正方形回路的线积分和和旋度$\nabla \times A$通过回路包围曲面的面积分,并验证两者相等。
一、线积分计算
1. 回路描述
正方形边长为2,位于$xy$平面),两边与$x$轴、$y$轴重合,四个顶点坐标为$(0,0,0)$、$(2,0,)$、$(2,2,)$、$(0,2,)$,回路方向为顺时针方向(根据答案积分路径)。
2. 分段积分
将回路分为四段,每段参数化并计算$A\cdot dl$:
- 段1:从$(0,0)$到$(2,0)$:$y=0$,$dl=e_xdx$,$A=e_xx$,积分:$\int_0^2 xdx$。
- 段2:从$(2,0)$到$(2,2)$:$x=2$,$dl=e_ydy$,$A=e_y2^2$,积分:$\int_^2 4dy$。
- 段3:从$(2,2)$到$(0,2)$:\y=2),$dl=-e_xdx$,$A=e_xx$,积分:$-\int_^2 xdx$。
- 段4:从$(0,2)$到$(0,0)$:\x=0),$dl=-e_ydy$,$A=e_y0^2$,积分:$\int_^2 0dy=0$。
3. 总积分
$\int_C A\cdot dl=\int_^2 xdx + \int_^2 4dy - \int_^2 xdx + 0 = 0 + 4\times2=8$。
二、旋度及面积分计算
1. 旋度$\nabla \times A$计算
矢量$A=e_xx + e_yx^2 + e_z y^2z$,旋度公式:
$\nabla \times A=\begin{vmatrix}e_x & e_y & e_z \\\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\x & x^2 & y^2z\end{vmatrix}=e_x\left(\frac{\partial(y^2z)}{\partial y}-\frac{\partial(x^2)}{\partial z}\right)-e_y\left(\frac{\partial(y^2z)}{\partial x}-\frac{\partial x}{\partial z}\right)+e_z\left(\frac{\partial x^2}{\partial x}-\frac{\partial x}{\partial y})$
化简得:$\nabla \times A=e_x(2yz) + e_y(0) + e_z(2x)$。
2. 面积分$\int_S (\nabla \times A)\cdot dS$
曲面$S$为$xy$平面正方形,$dS$的法向量$dS=e_z dxdy$,故:
$\int_S (\nabla \times A)\cdot dS=\int_S (e_z 2x)\cdot e_z dxdy=\int_^2\int_^2 2x dxdy$
积分:$\int_^2 dx \int_^2 2x dy= \int_^2 2x\cdot2x dx=4\int_^2 xdx=4\left[\frac{x^2}{2}\right]_^2=4\times2=8$。
三、斯托克斯定理验证
线积分$\int_C A\cdot dl=8$,面积分$\int_S \nabla \times A\cdot dS=8$,两者相等,验证成立。