(4) lim _(xarrow 0)dfrac (sin x-tan x)((sqrt [3]{1+{x)^2}-1)(sqrt (1+sin x)-1)}
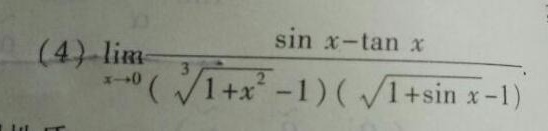
题目解答
答案
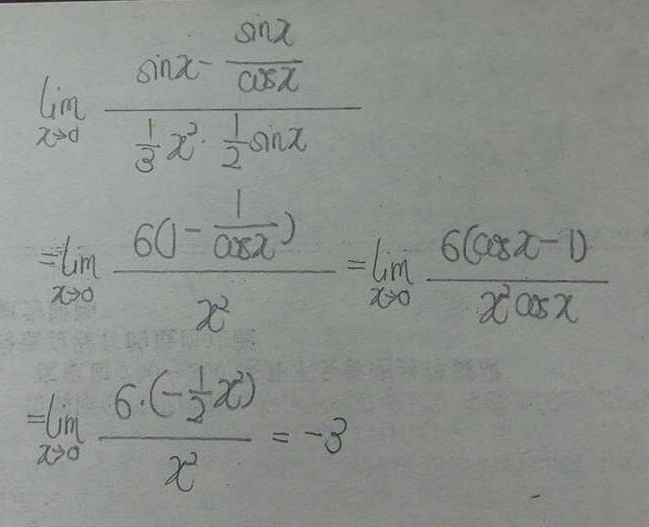
解析
考查要点:本题主要考查极限的计算,涉及等价无穷小替换和泰勒展开的应用,需要灵活处理分子和分母的展开式。
解题核心思路:
- 分子 $\sin x - \tan x$ 可变形为 $\sin x \cdot \frac{\cos x - 1}{\cos x}$,利用 $\cos x - 1 \sim -\frac{x^2}{2}$ 和 $\sin x \sim x$ 进行替换。
- 分母 分解为两部分:$\sqrt[3]{1+x^2} - 1$ 和 $\sqrt{1+\sin x} - 1$,分别用泰勒展开近似为 $\frac{1}{3}x^2$ 和 $\frac{1}{2}x$。
- 将分子和分母的主部代入,化简求极限。
破题关键点:
- 分子化简:将 $\tan x$ 表示为 $\frac{\sin x}{\cos x}$,通分后提取公共因子。
- 分母展开:对根式部分使用泰勒展开,保留主部项。
- 等价替换:利用 $\cos x - 1 \sim -\frac{x^2}{2}$ 和 $\sin x \sim x$ 简化计算。
分子部分
-
变形:
$\sin x - \tan x = \sin x - \frac{\sin x}{\cos x} = \sin x \left(1 - \frac{1}{\cos x}\right) = \sin x \cdot \frac{\cos x - 1}{\cos x}.$ -
等价无穷小替换:
当 $x \to 0$ 时,$\cos x - 1 \sim -\frac{x^2}{2}$,$\sin x \sim x$,$\cos x \sim 1$,因此:
$\sin x \cdot \frac{\cos x - 1}{\cos x} \sim x \cdot \frac{-\frac{x^2}{2}}{1} = -\frac{x^3}{2}.$
分母部分
-
三次根式展开:
$\sqrt[3]{1+x^2} - 1 = (1+x^2)^{1/3} - 1 \sim \frac{1}{3}x^2.$ -
平方根式展开:
$\sqrt{1+\sin x} - 1 = (1+\sin x)^{1/2} - 1 \sim \frac{1}{2}\sin x \sim \frac{1}{2}x.$ -
分母主部:
$\left(\frac{1}{3}x^2\right) \cdot \left(\frac{1}{2}x\right) = \frac{1}{6}x^3.$
整体极限
将分子和分母的主部代入:
$\lim_{x \to 0} \frac{-\frac{x^3}{2}}{\frac{1}{6}x^3} = \frac{-\frac{1}{2}}{\frac{1}{6}} = -3.$