题目
2.在对某大学的男生进行的调查中发现,喜欢踢足球的占92%,喜欢打篮球的占-|||-93%,在不喜欢踢足球的男生中有85%的人喜欢打篮球,现任选一名男生,求该生-|||-(1)喜欢踢足球或喜欢打篮球的概率;-|||-(2)不喜欢踢足球但喜欢打篮球的概率.

题目解答
答案
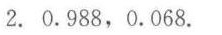
解析
考查要点:本题主要考查概率的并集、交集运算以及条件概率的应用。需要学生理解如何通过已知条件推导出关键概率值,并灵活运用概率公式进行计算。
解题核心思路:
- 明确事件关系:将“喜欢踢足球”和“喜欢打篮球”分别抽象为两个事件,利用集合运算关系建立公式。
- 条件概率转化:通过题目中“不喜欢踢足球的男生中有85%喜欢打篮球”的条件,结合全概率公式,求出关键的交集概率。
- 公式代换:利用概率的加法公式(并集公式)和事件分解,逐步推导最终结果。
破题关键点:
- 定义事件:设喜欢踢足球为事件$A$,喜欢打篮球为事件$B$,则$P(A)=0.92$,$P(B)=0.93$。
- 条件概率应用:通过$P(B|\neg A)=0.85$,结合公式$P(B \cap \neg A) = P(B|\neg A) \cdot P(\neg A)$,求出$\neg A$与$B$的交集概率。
- 事件分解:利用$P(B) = P(A \cap B) + P(B \cap \neg A)$,求出$P(A \cap B)$,再代入并集公式$P(A \cup B) = P(A) + P(B) - P(A \cap B)$。
第(1)题:喜欢踢足球或喜欢打篮球的概率
定义事件与已知条件
- 设事件$A$为“喜欢踢足球”,则$P(A) = 0.92$,因此$P(\neg A) = 1 - 0.92 = 0.08$。
- 设事件$B$为“喜欢打篮球”,则$P(B) = 0.93$。
- 已知在$\neg A$中,喜欢打篮球的比例为$P(B|\neg A) = 0.85$。
计算$P(B \cap \neg A)$
根据条件概率公式:
$P(B \cap \neg A) = P(B|\neg A) \cdot P(\neg A) = 0.85 \cdot 0.08 = 0.068$
计算$P(A \cap B)$
根据事件分解:
$P(B) = P(A \cap B) + P(B \cap \neg A) \implies P(A \cap B) = P(B) - P(B \cap \neg A) = 0.93 - 0.068 = 0.862$
计算$P(A \cup B)$
根据并集公式:
$P(A \cup B) = P(A) + P(B) - P(A \cap B) = 0.92 + 0.93 - 0.862 = 0.988$
第(2)题:不喜欢踢足球但喜欢打篮球的概率
直接利用第(1)题中计算的$P(B \cap \neg A)$:
$P(B \cap \neg A) = 0.068$