题目
求:lim _(xarrow 0)dfrac (4{x)^3-2(x)^2+x}(3{x)^2+2x}-|||-__
求: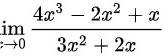
题目解答
答案
已知极限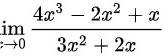 。
。
可以得到:令其分子为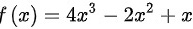 ,分母为
,分母为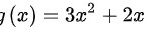 ,易知,
,易知,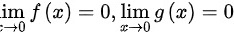 ,且
,且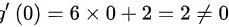 ,故极限
,故极限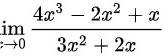 满足洛必达法则的条件:
满足洛必达法则的条件:
(1)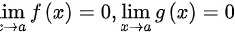
(2)在点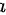 的某去心邻域内两者都可导,且
的某去心邻域内两者都可导,且 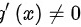 。
。
故有: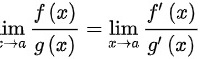 即:
即: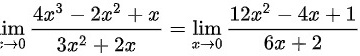
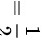
故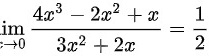 ,所以答案是
,所以答案是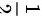 。
。
解析
考查要点:本题主要考查极限的计算方法,特别是洛必达法则的应用,以及代数式的因式分解技巧。
解题核心思路:
当直接代入$x=0$导致$\frac{0}{0}$型不定式时,可以考虑使用洛必达法则,即对分子和分母分别求导后再求极限。此外,也可以通过因式分解约简分式,直接代入求解。
破题关键点:
- 识别不定式类型:分子和分母在$x \to 0$时均趋近于$0$,属于$\frac{0}{0}$型不定式。
- 选择合适方法:既可以通过洛必达法则求导后计算,也可以通过提取公因式约分简化分式。
方法一:洛必达法则
-
验证条件:
- 分子$f(x)=4x^3-2x^2+x$,$\lim_{x \to 0} f(x)=0$;
- 分母$g(x)=3x^2+2x$,$\lim_{x \to 0} g(x)=0$;
- 在$x=0$的去心邻域内,$f(x)$和$g(x)$均可导,且$g'(x)=6x+2 \neq 0$(当$x$接近$0$时,$g'(x) \approx 2 \neq 0$)。
-
应用洛必达法则:
$\lim_{x \to 0} \frac{f(x)}{g(x)} = \lim_{x \to 0} \frac{f'(x)}{g'(x)} = \lim_{x \to 0} \frac{12x^2 -4x +1}{6x +2}$ -
代入计算:
当$x=0$时,分子为$1$,分母为$2$,故极限值为$\frac{1}{2}$。
方法二:因式分解
-
提取公因式:
- 分子:$4x^3-2x^2+x = x(4x^2-2x+1)$;
- 分母:$3x^2+2x = x(3x+2)$。
-
约分简化:
$\frac{x(4x^2-2x+1)}{x(3x+2)} = \frac{4x^2-2x+1}{3x+2} \quad (x \neq 0)$ -
直接代入:
当$x=0$时,分子为$1$,分母为$2$,故极限值为$\frac{1}{2}$。