题目
5.设随机变量X的概率密度为 f(x)= . B. dfrac {1)(2) . C. dfrac (2)(3) . D. dfrac (3)(4)
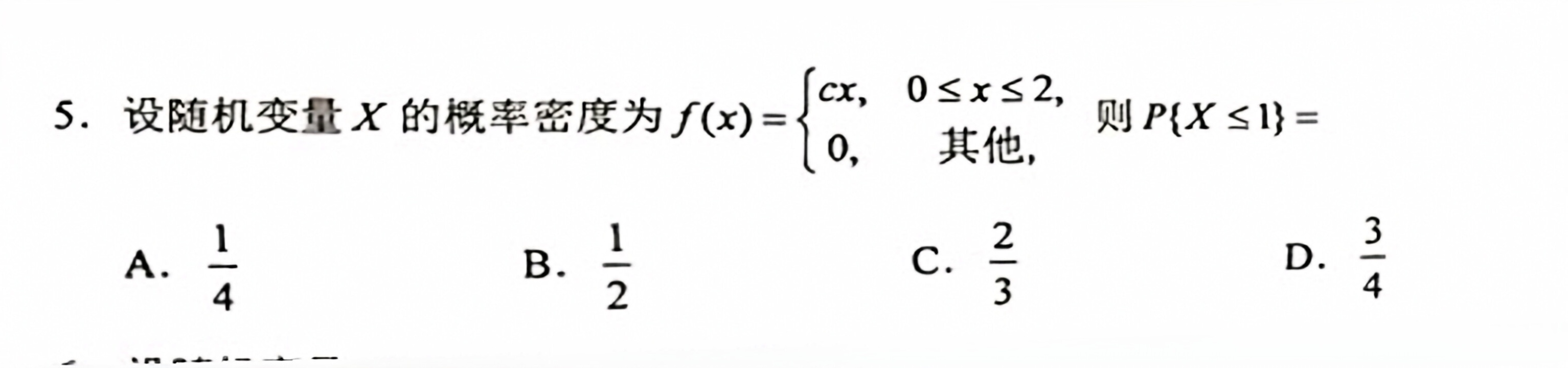
题目解答
答案

解析
本题主要考查概率密度函数的性质及概率的计算,具体步骤如下:
步骤1:利用概率密度函数的归一性求常数$c$
概率密度函数$f(x)$需满足$\int_{-\infty}^{+\infty}f(x)dx=1$。
已知$f(x)=\begin{cases}cx & (0\leq x x\leq2)\\0 & (其他)\end{cases}$,则:
$\int_{-\infty}^{+\infty}f(x)dx=\int_{0}^{2}cx\ dx=1$
计算积分:
$\int_{0}^{2}cx\ cx\ dx=c\cdot\left[\frac{x^2}{2}\right]_0^2=c\cdot\left(\frac{2^2}{2}-\frac{0^2}{2}}\right)=c\cdot2=2c$
令$2c=1$,解得$\(c=\frac{1}{2}$ )。
步骤2:计算$P\{X\leq1\}$
$\(P\{X\leq1\}=\int_{-\infty}^{1}f(x)dx$ ),因$x<0$时$f(x)=0$,故只需积分$\int_{0}^{1}cx\ dx$:
$\int_{0}^{1}\frac{1}{2}x\ dx=\frac{1}{2}\cdot\left[\frac{x^2}{2}\right]_0^1=\frac{1}{2}\cdot\left(\frac{1^2}{2}-0\right)=\frac{1}{4}
\$