题目
89. （0.7分）int sin 4xdx=dfrac (1)(4)int sin 4xdx=dfrac (1)(4)cos 4x+cA 正确B 错误
89. （0.7分）
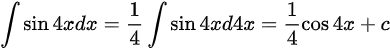
A 正确
B 错误
题目解答
答案
根据凑微分法的使用方法，在本题中，由于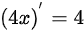
，因此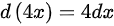
，
.
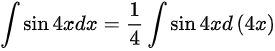由于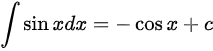
（
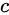为任意常数），则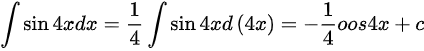
故原题中计算错误，故正确答案为：
B 错误
解析
步骤 1：识别积分形式
题目给出的积分是 $\int \sin 4x dx$，这是一个标准的三角函数积分形式，其中被积函数是 $\sin 4x$。
步骤 2：应用积分公式
根据积分公式，$\int \sin ax dx = -\frac{1}{a} \cos ax + C$，其中 $a$ 是常数，$C$ 是积分常数。在本题中，$a = 4$。
步骤 3：计算积分
将 $a = 4$ 代入积分公式，得到 $\int \sin 4x dx = -\frac{1}{4} \cos 4x + C$。
题目给出的积分是 $\int \sin 4x dx$，这是一个标准的三角函数积分形式，其中被积函数是 $\sin 4x$。
步骤 2：应用积分公式
根据积分公式，$\int \sin ax dx = -\frac{1}{a} \cos ax + C$，其中 $a$ 是常数，$C$ 是积分常数。在本题中，$a = 4$。
步骤 3：计算积分
将 $a = 4$ 代入积分公式，得到 $\int \sin 4x dx = -\frac{1}{4} \cos 4x + C$。