没数列(xn)有界,又 lim _(narrow infty )(y)_(n)=0.没数列(xn)有界,又 lim _(narrow infty )(y)_(n)=0..

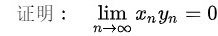 .
.
题目解答
答案
证:
因为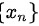 有界,故
有界,故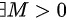 0" data-width="72" data-height="20" data-size="1151" data-format="png" style="max-width:100%">,使得对一切
0" data-width="72" data-height="20" data-size="1151" data-format="png" style="max-width:100%">,使得对一切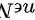 均有
均有
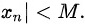
又 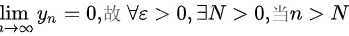 0,\exists N>0\text{,当}n>N" data-width="354" data-height="36" data-size="5236" data-format="png" style="max-width:100%">时,总有:
0,\exists N>0\text{,当}n>N" data-width="354" data-height="36" data-size="5236" data-format="png" style="max-width:100%">时,总有:
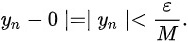
从而
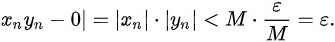
所以: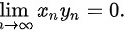
解析
考查要点:本题主要考查数列极限的乘积性质,特别是当一个数列有界且另一个数列极限为零时,它们的乘积的极限性质。
解题核心思路:
利用有界数列的性质和极限定义的结合。关键点在于通过有界数列的存在性,将乘积的绝对值转化为可控制的形式,再结合第二个数列极限为零的条件,找到合适的项数N,使得乘积的绝对值小于任意给定的正数ε。
破题关键点:
- 有界性:明确有界数列的存在性,即存在某个正数M,使得所有项的绝对值不超过M。
- 极限定义的应用:通过第二个数列极限为零的条件,找到对应的N,使得当n足够大时,第二个数列的绝对值被ε/M控制,从而保证乘积整体被ε控制。
证明步骤:
-
利用有界性确定M
因为数列$\{x_n\}$有界,根据定义,存在正数$M$,使得对一切自然数$n$,有
$|x_n| \leq M.$ -
应用极限定义控制$y_n$
已知$\lim\limits_{n \to \infty} y_n = 0$,根据极限定义,对任意给定的$\varepsilon > 0$,存在自然数$N$,当$n > N$时,有
$|y_n| < \frac{\varepsilon}{M}.$ -
结合两条件控制乘积
当$n > N$时,乘积的绝对值可估计为:
$|x_n y_n| = |x_n| \cdot |y_n| \leq M \cdot \frac{\varepsilon}{M} = \varepsilon.$ -
结论
根据极限定义,对任意$\varepsilon > 0$,存在$N$使得当$n > N$时,$|x_n y_n| < \varepsilon$,因此
$\lim\limits_{n \to \infty} x_n y_n = 0.$