题目
1.计算积分 (int )_(0)^1+i[ (x-y)+i(x)^2] dz, 积分路径(1)自原点至 1+i 的-|||-直线段;(2)自原点沿实轴至1,再由1铅直向上至 https:/img.zuoyebang.cc/zyb_ec39f02d15dc3a7b9e954f635c05fb57.jpg+i; (3)自原点沿-|||-虚轴至i,再由i沿水平方向向右至 https:/img.zuoyebang.cc/zyb_ec39f02d15dc3a7b9e954f635c05fb57.jpg+i.-|||-y-|||-y↑ y4-|||-1+i l+i i 1+i-|||-l2-|||-C2 l1-|||-0 x 0 →(C1) 1 x 0 x-|||-(1) (2) (3)

题目解答
答案
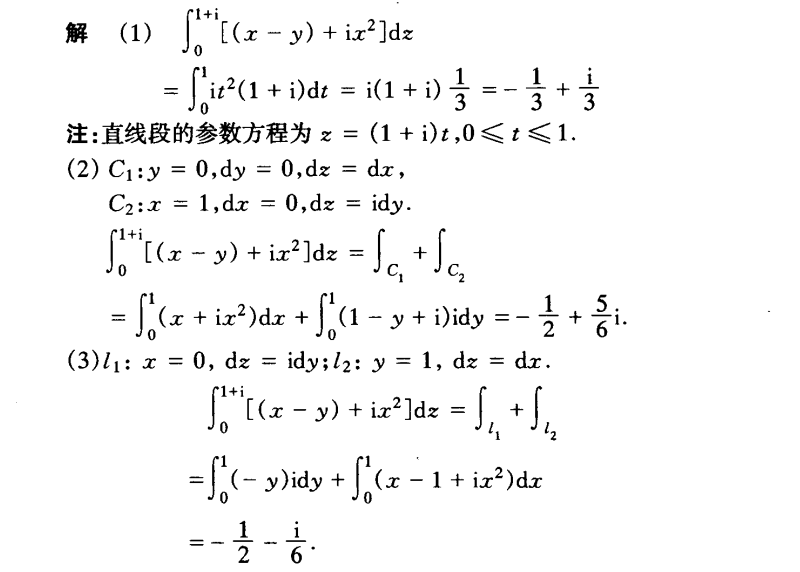
解析
本题考查复变函数的线积分计算,需沿不同路径计算积分。解题核心在于:
- 参数化积分路径,将复积分转化为实积分;
- 分段计算:对于分段路径,需分别计算各段积分再相加;
- 变量替换:根据路径参数方程,将被积函数中的变量用参数表示。
关键点:正确写出各路径的参数方程,注意积分路径中$dz$的表达式(如沿实轴$dz=dx$,沿虚轴$dz=idy$)。
(1) 直线段路径$z=(1+i)t$($0 \le t \le 1$)
- 参数化:$z = (1+i)t \Rightarrow x = t, y = t$,则$dz = (1+i)dt$;
- 代入被积函数:
$(x-y) + i x^2 = (t-t) + i t^2 = i t^2$ - 积分计算:
$\int_0^1 i t^2 \cdot (1+i) dt = i(1+i) \int_0^1 t^2 dt = i(1+i) \cdot \frac{1}{3} = -\frac{1}{3} + \frac{i}{3}$
(2) 分段路径$C_1$(实轴)+$C_2$(虚轴)
段$C_1$:$y=0$,$dz=dx$
- 被积函数:
$(x-0) + i x^2 = x + i x^2$ - 积分:
$\int_0^1 (x + i x^2) dx = \left[\frac{x^2}{2} + \frac{i x^3}{3}\right]_0^1 = \frac{1}{2} + \frac{i}{3}$
段$C_2$:$x=1$,$dz=idy$
- 被积函数:
$(1-y) + i \cdot 1^2 = (1-y) + i$ - 积分:
$\int_0^1 [(1-y) + i] \cdot i dy = \int_0^1 [i(1-y) - 1] dy = \frac{i}{2} - 1$ - 总积分:
$\frac{1}{2} + \frac{i}{3} + \frac{i}{2} - 1 = -\frac{1}{2} + \frac{5i}{6}$
(3) 分段路径$l_1$(虚轴)+$l_2$(水平线)
段$l_1$:$x=0$,$dz=idy$
- 被积函数:
$(0-y) + i \cdot 0^2 = -y$ - 积分:
$\int_0^1 (-y) \cdot i dy = -i \int_0^1 y dy = -\frac{i}{2}$
段$l_2$:$y=1$,$dz=dx$
- 被积函数:
$(x-1) + i x^2$ - 积分:
$\int_0^1 (x-1 + i x^2) dx = \left[\frac{x^2}{2} - x + \frac{i x^3}{3}\right]_0^1 = -\frac{1}{2} + \frac{i}{3}$ - 总积分:
$-\frac{i}{2} - \frac{1}{2} + \frac{i}{3} = -\frac{1}{2} - \frac{i}{6}$