题目
以 y=x 2-e x和 y=x 2-e x为特解的一阶非齐次线性微分方程为_____.
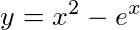 和
和
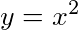 为特解的一阶非齐次线性微分方程为_____.
为特解的一阶非齐次线性微分方程为_____.
题目解答
答案
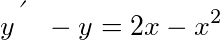 .
.
解析
考查要点:本题主要考查根据给定特解构造一阶非齐次线性微分方程的能力,需要理解微分方程解的结构及待定系数法的应用。
解题核心思路:
- 确定微分方程形式:一阶非齐次线性微分方程的标准形式为 $y' + P(x)y = Q(x)$,其中 $P(x)$ 和 $Q(x)$ 为待定函数。
- 代入特解求参数:将两个特解分别代入方程,建立关于 $P(x)$ 和 $Q(x)$ 的方程组,通过联立求解确定 $P(x)$ 和 $Q(x)$。
- 验证解的合理性:确保所求方程同时满足两个特解。
破题关键点:
- 利用特解差求齐次方程:两个特解的差应为对应齐次方程的解,从而快速确定 $P(x)$。
- 联立方程消元:通过代入两个特解,消去 $Q(x)$,直接解出 $P(x)$。
设所求微分方程为 $y' + P(x)y = Q(x)$,其中 $P(x)$ 和 $Q(x)$ 为待定函数。
代入特解 $y = x^2$
- 计算导数:$y' = 2x$。
- 代入方程:$2x + P(x) \cdot x^2 = Q(x)$。
代入特解 $y = x^2 - e^x$
- 计算导数:$y' = 2x - e^x$。
- 代入方程:$(2x - e^x) + P(x) \cdot (x^2 - e^x) = Q(x)$。
联立方程求解
将两个方程联立:
$\begin{cases}2x + P(x) \cdot x^2 = Q(x) \\2x - e^x + P(x) \cdot (x^2 - e^x) = Q(x)\end{cases}$
消去 $Q(x)$:
将第一个方程中的 $Q(x)$ 代入第二个方程:
$2x - e^x + P(x)(x^2 - e^x) = 2x + P(x)x^2$
化简方程:
左右两边相减得:
$-e^x + P(x)(-e^x) = 0 \implies P(x) = -1$
求 $Q(x)$:
将 $P(x) = -1$ 代入第一个方程:
$Q(x) = 2x + (-1) \cdot x^2 = 2x - x^2$
结论:微分方程为 $y' - y = 2x - x^2$。