题目
(7)(2006年,4分)设函数 y=f(x) 具有二阶导数,且 '(x)gt 0 ''(x)gt 0 Delta x 为自变量x-|||-在点x0处的增量, Delta y 与dy分别为f(x)在点x0处对应的增量与微分,若 Delta xgt 0, 则 ()-|||-(A) lt dylt Delta y (B) lt Delta ylt dy-|||-(C) Delta ylt dylt 0 (D) lt Delta ylt 0

题目解答
答案
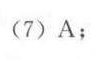
解析
本题主要考察函数的微分、增量以及导数的几何意义,关键是利用导数的正负判断函数的单调性与凹凸性,进而比较增量$\Delta y$与微分$dy$的大小。
步骤1:明确微分与增量的定义
- 函数$y=f(x)$在点$x_0$处的微分:$dy=f'(x_0)\Delta x$(线性近似)。
- 函数增量:$\Delta y=f(x_0+\Delta x)-f(x_0)$(实际变化量)。
- 由拉格朗日中值定理:$\Delta y=f'(x_0+\theta\Delta x)\Delta x$($0<\theta<1$)。
步骤2:利用导数性质比较$dy$与$\Delta y$
已知$f'(x)>0$(函数单调递增)且$f''(x)>0$(函数凹向上,导数单调递增):
- 因为$x_0+\theta\Delta x>x_0$($\Delta x>0$),且$f'(x)$单调递增,故$f'(x_0+\theta\Delta x)>f'(x_0)$。
- 两边同乘$\Delta x>0$,得:$f'(x_0+\theta\Delta x)\Delta x>f'(x_0)\Delta x$,即$\Delta y>dy$。
步骤3:判断$dy$的正负
因$f'(x_0)>0$且$\Delta x>0$,故$dy=f'(x_0)\Delta x>0$。
结论
$0