题目
2.解微分方程:-|||-(4) dfrac (dy)(dx)=dfrac (y)(x+{y)^2};

题目解答
答案
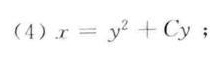
解析
步骤 1:分离变量
给定的微分方程是 $\dfrac {dy}{dx}=\dfrac {y}{x+{y}^{2}}$。我们首先尝试分离变量,即把方程写成 $f(y)dy = g(x)dx$ 的形式。为此,我们对原方程两边同时乘以 $(x+y^2)$,得到 $(x+y^2)dy = ydx$。然后,我们把方程重新写为 $\dfrac{dy}{y} = \dfrac{dx}{x+y^2}$。
步骤 2:积分
接下来,我们对两边进行积分。左边是关于 $y$ 的积分,右边是关于 $x$ 的积分。左边的积分是 $\int \dfrac{1}{y} dy = \ln|y| + C_1$,其中 $C_1$ 是积分常数。右边的积分需要一些技巧,我们注意到如果设 $u = x + y^2$,则 $du = dx + 2ydy$。但是,由于我们已经分离了变量,我们直接对右边进行积分,得到 $\int \dfrac{dx}{x+y^2} = \int \dfrac{dx}{u} = \ln|u| + C_2 = \ln|x+y^2| + C_2$,其中 $C_2$ 是积分常数。
步骤 3:合并常数并求解
将两边的积分结果合并,我们得到 $\ln|y| = \ln|x+y^2| + C$,其中 $C = C_2 - C_1$ 是新的常数。为了简化,我们可以将等式两边的对数去掉,得到 $|y| = e^C|x+y^2|$。由于 $e^C$ 是一个正数,我们可以将其表示为一个新的常数 $C$,即 $y = C(x+y^2)$。最后,我们整理得到 $x = y^2 + Cy$。
给定的微分方程是 $\dfrac {dy}{dx}=\dfrac {y}{x+{y}^{2}}$。我们首先尝试分离变量,即把方程写成 $f(y)dy = g(x)dx$ 的形式。为此,我们对原方程两边同时乘以 $(x+y^2)$,得到 $(x+y^2)dy = ydx$。然后,我们把方程重新写为 $\dfrac{dy}{y} = \dfrac{dx}{x+y^2}$。
步骤 2:积分
接下来,我们对两边进行积分。左边是关于 $y$ 的积分,右边是关于 $x$ 的积分。左边的积分是 $\int \dfrac{1}{y} dy = \ln|y| + C_1$,其中 $C_1$ 是积分常数。右边的积分需要一些技巧,我们注意到如果设 $u = x + y^2$,则 $du = dx + 2ydy$。但是,由于我们已经分离了变量,我们直接对右边进行积分,得到 $\int \dfrac{dx}{x+y^2} = \int \dfrac{dx}{u} = \ln|u| + C_2 = \ln|x+y^2| + C_2$,其中 $C_2$ 是积分常数。
步骤 3:合并常数并求解
将两边的积分结果合并,我们得到 $\ln|y| = \ln|x+y^2| + C$,其中 $C = C_2 - C_1$ 是新的常数。为了简化,我们可以将等式两边的对数去掉,得到 $|y| = e^C|x+y^2|$。由于 $e^C$ 是一个正数,我们可以将其表示为一个新的常数 $C$,即 $y = C(x+y^2)$。最后,我们整理得到 $x = y^2 + Cy$。