题目
求由方程 ^3+2xy+(y)^3=0 所确定隐函数的导数 dfrac (dy)(dx)

题目解答
答案
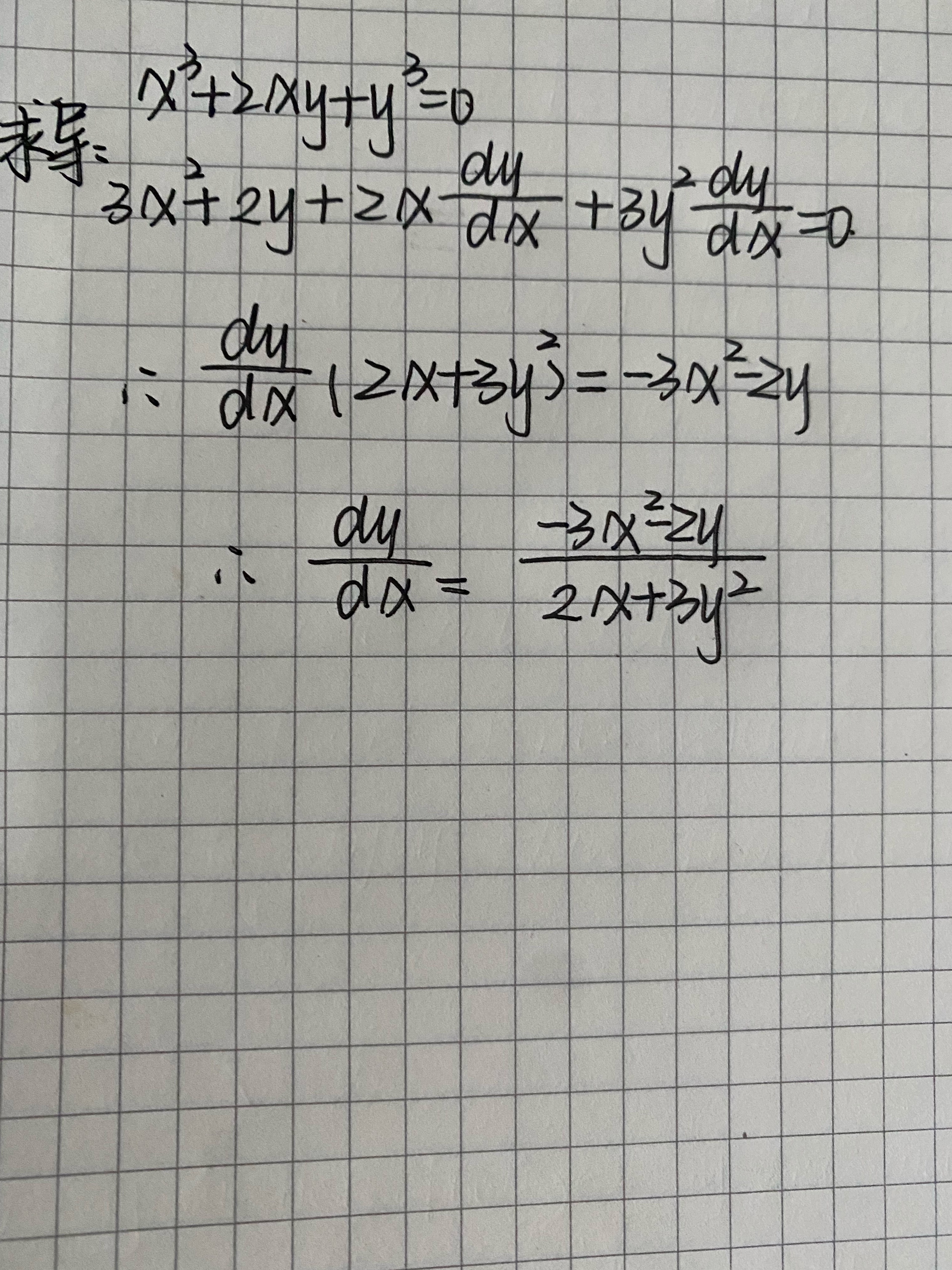
解析
步骤 1:对给定方程进行隐函数求导
对方程 ${x}^{3}+2xy+{y}^{3}=0$ 两边同时对 $x$ 求导,得到:
$3{x}^{2}+2y+2x\dfrac {dy}{dx}+3{y}^{2}\dfrac {dy}{dx}=0$
步骤 2:整理求导后的方程
将含有 $\dfrac {dy}{dx}$ 的项放在方程的一边,不含 $\dfrac {dy}{dx}$ 的项放在方程的另一边,得到:
$2x\dfrac {dy}{dx}+3{y}^{2}\dfrac {dy}{dx}=-3{x}^{2}-2y$
步骤 3:解出 $\dfrac {dy}{dx}$
将 $\dfrac {dy}{dx}$ 提取出来,得到:
$\dfrac {dy}{dx}(2x+3{y}^{2})=-3{x}^{2}-2y$
最后解出 $\dfrac {dy}{dx}$,得到:
$\dfrac {dy}{dx}=\dfrac {-3{x}^{2}-2y}{2x+3{y}^{2}}$
对方程 ${x}^{3}+2xy+{y}^{3}=0$ 两边同时对 $x$ 求导,得到:
$3{x}^{2}+2y+2x\dfrac {dy}{dx}+3{y}^{2}\dfrac {dy}{dx}=0$
步骤 2:整理求导后的方程
将含有 $\dfrac {dy}{dx}$ 的项放在方程的一边,不含 $\dfrac {dy}{dx}$ 的项放在方程的另一边,得到:
$2x\dfrac {dy}{dx}+3{y}^{2}\dfrac {dy}{dx}=-3{x}^{2}-2y$
步骤 3:解出 $\dfrac {dy}{dx}$
将 $\dfrac {dy}{dx}$ 提取出来,得到:
$\dfrac {dy}{dx}(2x+3{y}^{2})=-3{x}^{2}-2y$
最后解出 $\dfrac {dy}{dx}$,得到:
$\dfrac {dy}{dx}=\dfrac {-3{x}^{2}-2y}{2x+3{y}^{2}}$