题目
2、设f`(x)为连续函数,则 int (sin )^2xf'(cos x)dx-int cos xf(cos x)dx=
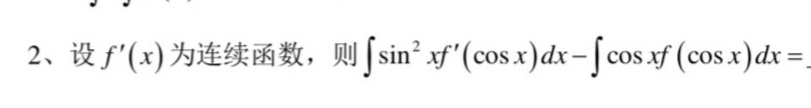
题目解答
答案

解析
本题考查不定积分的计算,主要运用分部积分法来求解。解题的关键在于合理选择分部积分公式中的$u$和$dv$,通过分部积分法对$\int \cos xf(\cos x)dx$进行变形,然后与$\int {\sin }^{2}xf'(\cos x)dx$进行化简计算。
- 首先对$\int \cos xf(\cos x)dx$使用分部积分法:
- 设$u = f(\cos x)$,$dv=\cos xdx$。
- 根据求导公式$(\cos x)^\prime=-\sin x$,对$u$求导可得$du = f'(\cos x)\cdot(-\sin x)dx$。
- 对$dv$积分可得$v=\int\cos xdx=\sin x$。
- 根据分部积分公式$\int u dv = uv-\int v du$,则$\int \cos xf(\cos x)dx=\sin xf(\cos x)-\int \sin x\cdot f'(\cos x)\cdot(-\sin x)dx$。
- 进一步化简为$\int \cos xf(\cos x)dx=\sin xf(\cos x)+\int {\sin }^{2}xf'(\cos x)dx$。
- 然后将上式代入原式$\int {\sin }^{2}xf'(\cos x)dx-\int \cos xf(\cos x)dx$:
- 可得$\int {\sin }^{2}xf'(\cos x)dx - (\sin xf(\cos x)+\int {\sin }^{2}xf'(\cos x)dx)$。
- 去括号得$\int {\sin }^{2}xf'(\cos x)dx - \sin xf(\cos x)-\int {\sin }^{2}xf'(\cos x)dx$。
- 合并同类项后结果为$-\sin xf(\cos x)+C$($C$为积分常数)。