题目
设平面图形由曲线y=1-x2(x≥0)及两坐标轴围成,求(1) 该平面图形绕x轴旋转所形成的旋转体体积(2) 求常数a的值,使直线y=a将该平面图形分成面积相等的两部分。
设平面图形由曲线y=1-x2(x≥0)及两坐标轴围成,求
(1) 该平面图形绕x轴旋转所形成的旋转体体积
(2) 求常数a的值,使直线y=a将该平面图形分成面积相等的两部分。
题目解答
答案
解:令y=0,解得x=-1,x=1
(1) 旋转体体积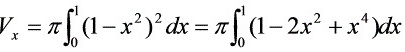
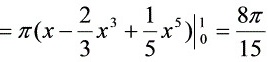
(2) 由题意得: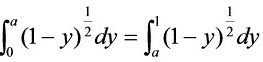 ,即
,即
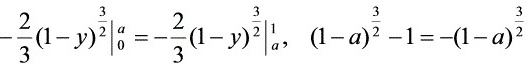
解得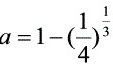
解析
考查要点:
- 旋转体体积计算:利用积分法求旋转体体积,掌握绕x轴旋转的体积公式。
- 面积等分问题:通过积分求平面图形的面积,并建立方程求解参数。
解题核心思路:
- 体积计算:将平面图形绕x轴旋转,使用圆盘法,积分被积函数为$πy^2$,积分区间为图形在x轴上的投影范围。
- 面积等分:将总面积分为两部分,通过积分建立方程,解方程求参数$a$。
破题关键点:
- 确定积分区间:曲线$y=1-x^2$($x \geq 0$)与坐标轴围成的区域,x范围为$[0,1]$。
- 变量替换:在面积等分问题中,将积分变量从$x$转换为$y$,简化计算。
第(1)题
旋转体体积
- 确定积分区间:曲线与x轴交点为$x=1$,积分区间为$[0,1]$。
- 应用圆盘法公式:体积$V = π\int_{0}^{1} y^2 dx = π\int_{0}^{1} (1-x^2)^2 dx$。
- 展开被积函数:$(1-x^2)^2 = 1 - 2x^2 + x^4$。
- 逐项积分:
$\int_{0}^{1} (1 - 2x^2 + x^4) dx = \left[ x - \frac{2}{3}x^3 + \frac{1}{5}x^5 \right]_{0}^{1} = 1 - \frac{2}{3} + \frac{1}{5} = \frac{8}{15}$ - 最终结果:$V = \frac{8π}{15}$。
第(2)题
求常数$a$使面积相等
- 总面积计算:
$S = \int_{0}^{1} (1-x^2) dx = \left[ x - \frac{x^3}{3} \right]_{0}^{1} = \frac{2}{3}$
每部分面积应为$\frac{1}{3}$。 - 转换积分变量:以$y$为变量,$x = \sqrt{1-y}$,积分区间为$[0,1]$。
- 建立方程:
$\int_{0}^{a} \sqrt{1-y} \, dy = \int_{a}^{1} \sqrt{1-y} \, dy$ - 计算积分:
$\int \sqrt{1-y} \, dy = -\frac{2}{3}(1-y)^{3/2} + C$ - 代入上下限:
$-\frac{2}{3}(1-a)^{3/2} + \frac{2}{3} = \frac{2}{3}(1-a)^{3/2}$ - 解方程:
$1 - (1-a)^{3/2} = (1-a)^{3/2} \implies (1-a)^{3/2} = \frac{1}{2} \implies a = 1 - \left( \frac{1}{4} \right)^{1/3}$