29.由下列各已知调和函数求解析函数 f(z)=u+iv =-|||-(1) =(x-y)((x)^2+4xy+(y)^2) ;-|||-(2) =dfrac (y)({x)^2+(y)^2} f(2)=0 ;-|||-(3) u=2(x-1)y f(2)=-i ;-|||-(4) =arctan dfrac (y)(x),xgt 0 -

题目解答
答案
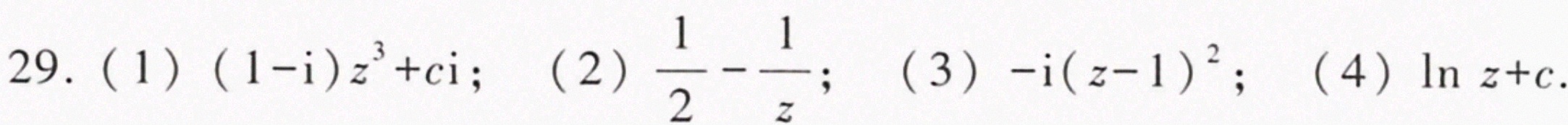
解析
题目考察知识
本题主要考察解析函数的性质及调和函数与解析函数的关系,核心知识点包括:
- 解析函数的充要条件(柯西-黎曼方程):若$f(z)=u(x,y)+iv(x,y)$解析,则$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}$,$\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$,且$u,v$均为调和函数(二阶偏导连续且满足拉普拉斯方程$\Delta u=\Delta v=0$)。
- 由调和函数求解析函数的方法:
- 若已知实部$u$,可通过积分柯西-黎曼方程求虚部$v$;
- 若已知虚部$v$,可通过积分柯西-黎曼方程求实部$u$;
- 利用复数形式的积分(如$f(z)=\int (u_x+iv_x)dz+C$)或变量替换$z=x+iy$简化计算。
各小题详细解析
(1) 已知$u=(x-y)(x^2+4xy+y^2)$,求$f(z)=u+iv$
步骤1:化简$u$的表达式
展开$u$:
$u=(x-y)(x^2+4xy+y^2)=x^3+4x^2y+xy^2-x^2y-4xy^2-y^3=x^3+3x^2y-3xy^2-y^3$
观察发现$u=\text{Re}((1-i)z^3)$,因为:
$(1-i)z^3=(1-i)(x+iy)^3=(1-i)(x^3+3x^2(iy)+3x(iy)^2+(iy)^3)=x^3+3x^2y-3xy^2-y^3+i(-x^3+3x^2y-3xy^2+y^3)$
其实部即为$u$,虚部为$v=-x^3+3x^2y-3xy^2+y^3$,满足柯西-黎曼方程。
步骤2:确定解析函数
故$f(z)=(1-i)z^3+C$,常数$C$为纯虚数(因实部已确定),记$C=ci$,得:
$f(z)=(1-i)z^3+ci$
(2) 已知$v=\frac{y}{x^2+y^2}$,$f(2)=0$,求$f(z)=u+iv$
步骤1:利用柯西-黎曼方程求$u$
已知$v=\frac{y}{x^2+y^2}$,则:
$\frac{\partial v}{\partial y}=\frac{(x^2+y^2)-y(2y)}{(x^2+y^2)^2}=\frac{x^2-y^2}{(x^2+y^2)^2}$
由$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}$,积分得:
$u=\int \frac{x^2-y^2}{(x^2+y^2)^2}dx+C(y)$
计算积分(令$t=x^2+y^2$,$dt=2xdx$):
$u=-\frac{x}{x^2+y^2}+C(y)$
再由$\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}$,$\frac{\partial v}{\partial x}=-\frac{2xy}{(x^2+y^2)^2}$,则:
$\frac{2xy}{(x^2+y^2)^2}+C'(y)=\frac{2xy}{(x^2+y^2)^2}\implies C'(y)=0\implies C(y)=C$
故$u=-\frac{x}{x^2+y^2}+C$,$f(z)=u+iv=C-\frac{x+iy}{x^2+y^2}=C-\frac{1}{z}$(因$\frac{1}{z}=\frac{x-iy}{x^2+y^2}$,故$\frac{x+iy}{x^2+y^2}=-\frac{1}{\overline{z}}$?不,纠正:$\frac{1}{z}=\frac{x-iy}{x^2+y^2}$,则$\overline{\frac{1}{z}}=\frac{x+iy}{x^2+y^2}$,但此处$u+iv=C-\frac{x+iy}{x^2+y^2}$,而$-\frac{1}{z}=-\frac{x-iy}{x^2+y^2}$,发现之前符号错?重新看:$v=\frac{y}{x^2+y^2}=\text{Im}\left(\frac{i}{z}\right)$,因$\frac{i}{z}=\frac{i(x-iy)}{x^2+y^2}=\frac{y+ix}{x^2+y^2}$,其实部为$\frac{y}{x^2+y^2}$?不,$\frac{i}{z}=\frac{y}{x^2+y^2}+i\frac{x}{x^2+y^2}$,故$v=\text{Im}\left(\frac{i}{z}\right)=\frac{x}{x^2+y^2}$,哦!题目$v=\frac{y}{x^2+y^2}$,则$v=\text{Im}\left(-\frac{i}{z}\right)$,因$-\frac{i}{z}=-\frac{i(x-iy)}{x^2+y^2}=-\frac{y+ix}{x^2+y^2}=-\frac{y}{x^2+y^2}-i\frac{x}{x^2+y^2}$,不对。换用$f(z)=u+iv$,$u=-\frac{x}{x^2+y^2}+C$,则$f(z)=C-\frac{x}{x^2+y^2}+i\frac{y}{x^2+y^2}=C-\frac{x-iy}{x^2+y^2}=C-\frac{1}{z}$(因$\frac{1}{z}=\frac{x-iy}{x^2+y^2}$),对!因为$-\frac{1}{z}=-\frac{x-iy}{x^2+y^2}=-\frac{x}{x^2+y^2}+i\frac{y}{x^2+y^2}$,其实部为$-\frac{x}{x^2+y^2}$,虚部为$\frac{y}{x^2+y^2}$,正好是$u+C$($C$为实常数)。
步骤2:用$f(2)=0$确定常数
$f(2)=C-\frac{1}{2}=0\implies C=\frac{1}{2}$,故:
$f(z)=\frac{1}{2}-\frac{1}{z}$
(3) 已知$u=2(x-1)y$,$f(2)=-i$,求$f(z)=u+iv$
步骤1:利用柯西-黎曼方程求$v$
$u=2(x-1)y$,则$\frac{\partial u}{\partial x}=2y$,$\frac{\partial u}{\partial y}=2(x-1)$。
由$\frac{\partial v}{\partial y}=\frac{\partial u}{\partial x}=2y$,积分得$v= y^2 + C(x)$。
由$\frac{\partial v}{\dx}=-\frac{\partial u}{\partial y}=-2(x-1)$,积分得$C(x)=-(x-1)^2 + C$,故:
$v=y^2-(x-1)^2+C$
则$f(z)=u+iv=2(x-1)y + i\left[y^2-(x-1)^2+C\right]=-i\left[(x-1)^2 - 2(x-1)y + y^2\right] + iC=-i(x-1-iy)^2 + iC=-i(z-1)^2 + iC$(因$z-1=(x-1)+iy$,\((z-1)^
\]
### (4) 已知$v=\arctan\frac{y}{x}(x>0)$,求$f(z)=u+iv$
步骤1:利用柯西-黎曼方程求$u$
$v=\arctan\frac{y}{x}(x>0)$,则$\frac{\partial v}{\partial y}=\frac{1}{1+(y/x)^2}\cdot\frac{1}{x}=\frac{x}{x^2+y^2}$,$\frac{\partial v}{\partial x}=\frac{1}{1+(y/x)^2}\cdot\left(-\frac{y}{x^2}\right)=-\frac{y}{x^2+y^2}$。
由$\frac{\partial u}{\partial x}=\frac{\partial v}{\partial y}=\frac{x}{x^2+y^2}$,积分得$u=\frac{1}{2}\ln(x^2+y^2)+C(y)$。
由$\frac{\partial u}{\partial y}=-\frac{\partial v}{\partial x}=\frac{y}{x^2+y^2}$,对$u$求导:$\frac{y}{x^2+y^2}+C'(y)=\frac{y}{x^2+y^2}\implies C'(y)=0\implies C(y)=C$。
故$u=\frac{1}{2}\ln(x^2+y^2)+C=\ln|z|+C$($x>0$时$|z|=z$),则:
$f(z)=\ln z + C$