根据数列极限定义证明：(1) lim _(narrow infty )dfrac (1)({n)^2}=0-|||-(2) lim _(narrow infty )dfrac (3n+1)(2n+1)=dfrac (3)(2) __-|||-(3) lim _(narrow infty )dfrac (sqrt {{n)^2+(a)^2}}(n)=1（4）(1) lim _(narrow infty )dfrac (1)({n)^2}=0-|||-(2) lim _(narrow infty )dfrac (3n+1)(2n+1)=dfrac (3)(2) __-|||-(3) lim _(narrow infty )dfrac (sqrt {{n)^2+(a)^2}}(n)=1
根据数列极限定义证明：
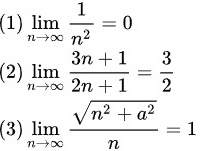
（4）
题目解答
答案
\frac{1}{\sqrt{\varepsilon}}. \\
&\text{取N} =\left[{\frac{1}{\sqrt{\varepsilon}}}\right],\text{只要 }n>N,\text{就有} \\
&\left|\frac{1}{n^{2}}-0\right|<\varepsilon \\
&\text{因此} \lim_{n\rightarrow\infty}\frac{1}{n^{2}}=0
\end{aligned}" data-width="660" data-height="209" data-size="18659" data-format="png" style="max-width:100%">
0,\text{要使}\left|\frac{3n+1}{2n+1}-\frac{3}{2}\right|<\varepsilon,\text{只要}\frac{1}{n}<\varepsilon,\text{即 }n>\frac{1}{\varepsilon}. \\
& \text{于是取}N=\left[{\frac{1}{\varepsilon}}\right],\text{只要 }n>N,\text{就有} \\
&\left|\frac{3n+1}{2n+1}-\frac{3}{2}\right|<\varepsilon \\
&\lim_{n\to\infty}\frac{3n+1}{2n+1}=\frac32
\end{aligned}" data-width="481" data-height="344" data-size="29341" data-format="png" style="max-width:100%">
0,\textit{要使}\left|\frac{\sqrt{n^{2}+a^{2}}}{n}-1\right|<\varepsilon,\text{只要}\frac{a^{2}}{n}<\varepsilon,\text{即 }n>\frac{a^{2}}{\varepsilon}, \\
\text{于是取 }N=\left[\frac{a^{2}}{\varepsilon}\right].\text{ 只要 }n>N,\text{就有} \\
\left|\frac{\sqrt{n^{2}+a^{2}}}{n}-1\right|<\varepsilon \\
\text{因此},\quad\lim_{n\to\infty}\frac{\sqrt{n^{2}+u^{2}}}{n}=1
\end{aligned}" data-width="525" data-height="373" data-size="29950" data-format="png" style="max-width:100%">
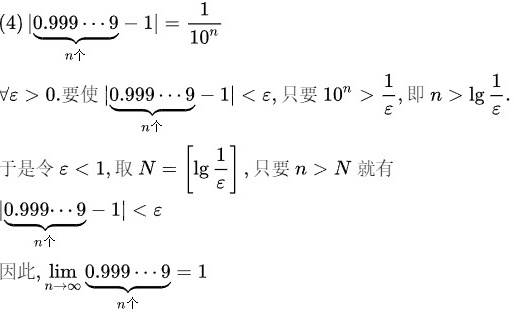0.\text{要使 }|\underbrace{0.999\cdots9}_{n\text{个}} -1|<\varepsilon,\text{只要 }10^n>\frac1\varepsilon,\text{即 }n>\lg\frac1\varepsilon. \\
&\text{于是令 }\varepsilon<1,\text{取 }N=\left [\lg\frac1\varepsilon \right ],\text{只要 }n>N\text{ 就有} \\
&|\underbrace{0.999\cdotp\cdotp\cdotp9}_{n\text{个}} - 1 | < \varepsilon \\
&\text{因此,}\lim_{n\to\infty}\underbrace{0.999\cdots9}_{n\text{个}} = 1
\end{aligned}" data-width="519" data-height="318" data-size="24550" data-format="png" style="max-width:100%">
解析
要证明数列 $\dfrac {1}{{n}^{2}}$ 的极限为0，根据数列极限的定义，对于任意的 $\varepsilon > 0$，存在正整数 $N$，使得当 $n > N$ 时，有 $\left|\dfrac {1}{{n}^{2}} - 0\right| < \varepsilon$。即 $\dfrac {1}{{n}^{2}} < \varepsilon$，从而 $n > \dfrac {1}{\sqrt{\varepsilon}}$。取 $N = \left[\dfrac {1}{\sqrt{\varepsilon}}\right]$，则当 $n > N$ 时，有 $\left|\dfrac {1}{{n}^{2}} - 0\right| < \varepsilon$。
步骤 2：证明 $\lim _{n\rightarrow \infty }\dfrac {3n+1}{2n+1}=\dfrac {3}{2}$
要证明数列 $\dfrac {3n+1}{2n+1}$ 的极限为 $\dfrac {3}{2}$，根据数列极限的定义，对于任意的 $\varepsilon > 0$，存在正整数 $N$，使得当 $n > N$ 时，有 $\left|\dfrac {3n+1}{2n+1} - \dfrac {3}{2}\right| < \varepsilon$。即 $\left|\dfrac {6n+2-6n-3}{2(2n+1)}\right| = \dfrac {1}{2(2n+1)} < \dfrac {1}{2n+1} < \dfrac {1}{n} < \varepsilon$，从而 $n > \dfrac {1}{\varepsilon}$。取 $N = \left[\dfrac {1}{\varepsilon}\right]$，则当 $n > N$ 时，有 $\left|\dfrac {3n+1}{2n+1} - \dfrac {3}{2}\right| < \varepsilon$。
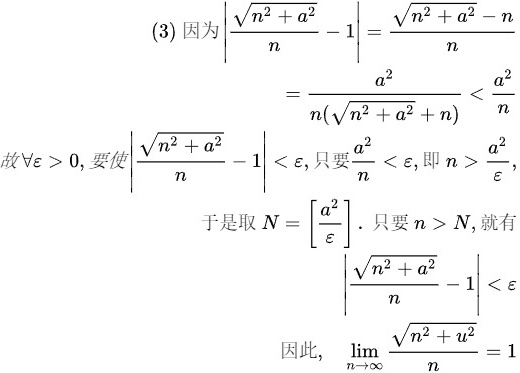
步骤 3：证明 $\lim _{n\rightarrow \infty }\dfrac {\sqrt {{n}^{2}+{a}^{2}}}{n}=1$
要证明数列 $\dfrac {\sqrt {{n}^{2}+{a}^{2}}}{n}$ 的极限为1，根据数列极限的定义，对于任意的 $\varepsilon > 0$，存在正整数 $N$，使得当 $n > N$ 时，有 $\left|\dfrac {\sqrt {{n}^{2}+{a}^{2}}}{n} - 1\right| < \varepsilon$。即 $\dfrac {a^{2}}{n(\sqrt {{n}^{2}+{a}^{2}}+n)} < \dfrac {a^{2}}{n} < \varepsilon$，从而 $n > \dfrac {a^{2}}{\varepsilon}$。取 $N = \left[\dfrac {a^{2}}{\varepsilon}\right]$，则当 $n > N$ 时，有 $\left|\dfrac {\sqrt {{n}^{2}+{a}^{2}}}{n} - 1\right| < \varepsilon$。
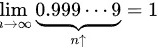
步骤 4：证明 $\lim _{n\rightarrow \infty }0.999\cdots 9=1$
要证明数列 $0.999\cdots 9$ 的极限为1，根据数列极限的定义，对于任意的 $\varepsilon > 0$，存在正整数 $N$，使得当 $n > N$ 时，有 $\left|0.999\cdots 9 - 1\right| < \varepsilon$。即 $\dfrac {1}{10^{n}} < \varepsilon$，从而 $n > \lg \dfrac {1}{\varepsilon}$。取 $N = \left[\lg \dfrac {1}{\varepsilon}\right]$，则当 $n > N$ 时，有 $\left|0.999\cdots 9 - 1\right| < \varepsilon$。