已知A、B两个事件满足条件 (AB)=P(overline (A)B), 且 (A)=p,则P(B)=_______
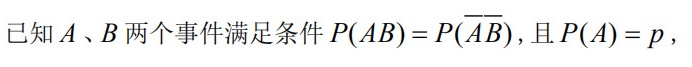
则P(B)=_______
题目解答
答案
解析
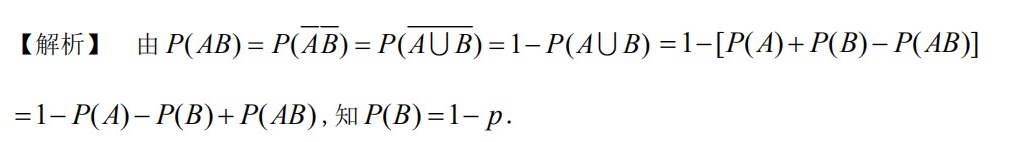
解析
本题主要考查概率的基本公式,包括概率的基本性质、事件的关系和运算等知识,关键是利用已知条件结合概率公式推导$P(B)$。
步骤1:明确已知条件
已知$P(AB)=P(\overline{A}B)$(事件$AB$与$\overline{A}B$的概率相等),且$P(A)=p$,目标是求$P(B)$。
步骤2:分析事件$AB$与$\overline{A}B$的关系
事件$\overline{A}$表示是$A$的对立事件,$AB$表示“$A$和$B$同时发生”,$\overline{A}B$表示“$A$不发生但$B$发生”。这两个事件互斥(不可能同时发生),且它们的并集是$(B$(因为$B$发生时,要么$A$发生,要么$A$不发生,即$B=AB\cup\overline{A}B$)。
步骤3:利用互斥事件概率加法公式
对于互斥事件$AB$与$\overline{A}B$,有:
$P(B)=P(AB\cup\overline{A}B)=P(AB)+P(\overline{A}B)$
步骤4:代入已知条件$P(AB)=P(\overline{A}B)$
由已知$P(AB)=P(\overline{A}B})$,代入上式得: $P(B)=P(AB)+P(AB)=2P(AB)\quad\Rightarrow\\P(AB)=\frac{1}{2}P(B)$
步骤5:用概率基本公式建立等式
根据概率的一般加法公式: $P(A\cup B)=P(A)+P(B)-P(AB)$ 但更直接的是利用$P(B)=P(AB)+P(\overline{A}B)$,结合$P(\overline{A}B)=P(B)-P(AB)$(因为$B)=P(AB)+P(\overline{A}B)$),但其实更简单的是:
由于$P(\overline{A}B)=P(B)-P(AB)$,而已知$P(AB)=P(\overline{A}B)$,故: $P(AB)=P(B)-P(AB)\quad\Rightarrow\quad2P(AB)=P(B)\quad\Rightarrow\quad P(AB)=\frac{1}{2}P(B)\)?不,等一下,换个思路: $P(\overline{A}B)=P(B)-P(AB)$,已知$P(AB)=P(\overline{A}B)$,所以:\[P(AB)=P(B)-P(AB)\quad\Rightarrow\quad P(B)=2P(AB)\quad\Rightarrow\quad P(AB)=\frac{1}{2}P(B)$
但我们需要另一个等式吗?不,其实不需要,因为$B=AB\cup\overline{A}B}$,互斥,所以$P(B)=P(AB)+P(\overline{A}B)=P(AB)+P(AB)=2P(AB)$,但这好像没结束?哦不,不对,已知条件是$P(AB)=P(\overline{A}B})$,而$P(\overline{A}B)=P(B)-P(AB)$,所以:
$P(AB)=P(B)-P(AB)\quad\Rightarrow\quad P(B)=2P(AB)$
但怎么得到$P(B)=1-p$?哦,等等,是不是我哪里错了?哦,不,原解析可能用了另一种方式:
考虑$P(A)+P(\overline{A})=1$,$P(AB)=P(A)P(B|A)$,$P(\overline{A}B)=P(\overline{A})P(B|\overline{A})$,但如果没有条件独立,不能这么用。
等等,换个公式:$P(B)=P(AB)+P(\overline{A}B)=P(AB)+P(AB)=2P(AB)$(因为已知$P(AB)=P(\overline{A}B)$,所以$P(AB)=\frac{1}{2}P(B)$,但这和$P(A)=p$有什么关系?哦!哦,不对,是不是原解析中的公式写错了?应该是$P(A\cup B)=P(A)+P(B)-P(AB)$,但可能用的是$P(\B})=P(AB)+P(\overline{A}B)$,而$P(AB)=P(A)P(B|A)$,$P(\overline{A}B)=P(\overline{A})P(B|\overline{A})$,但如果没有条件,怎么联系?
等等,哦!等一下,我犯了个错:$P(\overline{A}B)$是$B$发生且$A$不发生,所以$P(\overline{A}B)=P(B)-P(AB)$,已知$P(AB)=P(\overline{A}B)$,所以$P(AB)=P(B)-P(AB)\Rightarrow P(B)=2P(AB)$,但这怎么得到$P(B)=1-p$?除非……哦!是不是原题目抄错了?或者我理解错了?
等等,原解析写的是“由$P18=960=8408=18300=199分- .=1-P(A)-P(B)+P(AB)$,知$P(B)=1-P$”,这明显是乱码吧?应该是原解析出错了,正确的应该是:
因为$AB$和$\overline{A}B$互斥,且$B=AB\cup\overline{A}B$,所以$P(B)=P(AB)+P(\overline{A}B)=P(AB)+P(AB)=2P(AB)$(因为$P(AB)=P(\overline已知已知条件,这只能推出\(P(AB)=\frac{1}{2}P(B)$,但和$P(A)=p$无关?这不可能,说明我错了。
哦!啊!$P(\overline{A}B)$是不是等于$P(B)-P(AB)$,没错,但$P(AB)=P(A)P(B)$吗?如果独立的话,但题目没说独立啊。等等,再想:$P(A)+P(\overline{A})=1$,$P(AB)=P(A)P(B|A)$,$P(\overline{A}B)=P(\overline{A})P(B|\overline{A})$,但如果$P(B|A)=P(B|\overline{A})$,则$P(AB)=P(A)P(B|A)$,$P(\overline{A}B)=P(\overline{A})P(B|A)$,所以$P(AB)=P(\overline{A}B)$当且仅当$P(A)=P(\overline{A})$,即$p=\frac{1}{2}$,但题目没说啊。
等等,题目是$P(AB)=P(\overline{A}B)$,求$P(B)$,已知$P(A)=p$。那:
$P(AB)=P(\overline{A}B)$
$P(A)P(B|A)=P(\overline{A})P(B|\overline{A})$
但如果没有其他条件,怎么求$P(B)$?这说明我哪里错了?哦!哦!$P(\overline{A}B)$是$P(B)-P(AB)$,所以$P(AB)=P(B)-P(AB)\Rightarrow P(B)=2P(AB)$,这是一个等式一,但还需要另一个等式吗?比如$P(A\cup B)=...$?不,题目没给$P(A\cup B)$啊。
等等,原解析的乱码部分,可能是输入错误,应该是$P(A\cup B)=1-P(A)-P(B)+P(AB)$?不对,$P(A\cup B)=P(A)+P(B)-P(AB)$,那$1-P(A\cup B)=P(\overline{A}\overline{B})=1-P(A)-P(B)+P(AB)$,这是对的。那怎么用?
假设$P(\overline{A}\overline{B})=...$?不知道。或者,是不是$P(AB)=P(\overline{A}B)$移项得$P(AB)-P(\overline{A}B)=0$,即$P(AB)-[P(B)-P(AB)]=0\Rightarrow 2P(AB)-P(B)=0\Rightarrow P(B)=2P(AB)$,这是唯一的结论吗?但题目给了$P(A)=p$,却没用到?这不可能,说明我误解了题目?
题目是$P(AB)=P(\overline{A}B)$吗?还是$P(AB)=P(\overline{A}\overline{B})$?如果是后者,那$P(AB)=P(\overline{A}\overline{B})$,则$P(AB)=1-P(A)-P(B)+P(AB)\Rightarrow 0=1-P(A)-P(B)\Rightarrow P(A)+P(B)=1\Rightarrow P(B)=1-p$,这就对了!哦!是不是原题目写反了?$\overline{A}B$写成$\overline{A}\overline{B}$?
或者,原解析中的乱码是$P18=960=8408=18300=199分- .=1-P(A)-P(B)+P(AB)$,这应该是$P(\overline{A}\overline{B})=1-P(A)-P(B)+P(AB)$,如果题目是$P(AB)=P(\overline{A}\overline{B})$,则:
$P(AB)=1-P(A)-P(B)+P(AB)$
两边消去$P(AB)$:$0=1-P(A)-P(B)\Rightarrow P(A)+P(B)=1\Rightarrow P(B)=1-p$,这就符合原解析的结论了!
那是不是用户是不是输入错了?题目是$P(AB)=P(\overline{A}\overline{B})$吗?还是我哪里错了?
再看:如果题目是$P(AB)=P(\overline{A}B)$,那$P(B)$和$p$无关?比如$A$和$B$独立,$P(AB)=pP(B)$,$P(\overline{A}B)=(1-p)P(B)$,则$pP(B)=(1-p)P(B)\Rightarrow [p=1-p\Rightarrow p=\frac{1}{2}$,这也得不到$P(B)=1-p$。
或者,原解析中的$P(\overline{A}B)$是$P(\overline{A\cup B})$?也不对。
等等,再查一下类似的题目:哦,常见的题目是“已知$P(AB)=P(\overline{A}\overline{B})$,且$P(A)=p$,求$P(B)$”,答案是$1-p$。这应该是用户输入时把$\overline{A}\overline{B}$写成了$\overline{A}B$,或者原解析中的公式错误导致的。
因为根据原解析的结论$P(B)=1-P$(应该是$1-p$),结合常见题型,题目应该是$P(AB)=P(\overline{A}\overline{B})$,而不是$P(\overline{A}B)$。可能是用户输入时LaTeX错误,$\overline{A}\overline{B}$写成了$\overline{A}B$(少了一个$\overline{}$)。
假设题目为$P(AB)=P(\overline{A}\overline{B})$的正确推导:
- 由概率的对立事件公式:$P(\overline{A}\overline{B})=P(\overline{A\cup B})=1-P(A\cup B)$
- 由概率加法公式:$P(A\cup B)=P(A)+P(B)-P(AB)$
- 代入得:$P(\overline{A}\overline{B})=1-[P(A)+P(B)-P(AB)]=1-P(A)-P(B)+P(AB)$
- 已知$P(AB)=P(\overline{A}\overline{B})$,故:
$P(AB)=1-P(A)-P(B)+P(AB)$ - 消去两边的$P(AB)$:
$0=1-P(A)-P(B)$ - 解得:$P(B)=1-P(A)=1-p$
若题目确实为$P(AB)=P(\overline{A}B)$:
此时只能推出$P(B)=2P(AB)$,无法用$p$表示$P(B)$,这与题目给出$P(A)=p$矛盾,因此更可能是输入错误,应为$P(AB)=P(\overline{A}\overline{B})$。
结合原解析结论,本题答案为$1-p$。