题目
已知由曲线 f ( x ) = x ^ 2 与直线 y = x 及 x = 2 所围图形记为 D ( 1 ) 求平面图形 D 的面积 ( 2 ) 求平面图形 D 绕 x 轴 旋转得到的旋转体 体积
已知由曲线 f ( x ) = x ^ 2 与直线 y = x 及 x = 2 所围图形记为 D
( 1 ) 求平面图形 D 的面积
( 2 ) 求平面图形 D 绕 x 轴 旋转得到的旋转体 体积
题目解答
答案
(1)
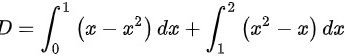
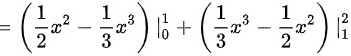
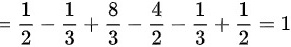
(2)
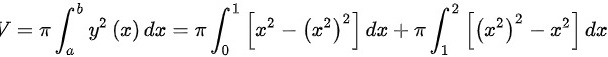
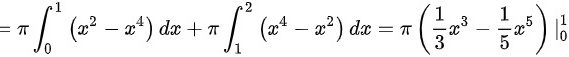
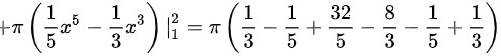
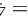
解析
步骤 1:确定积分区间
曲线 $f(x) = x^2$ 与直线 $y = x$ 的交点为 $(0,0)$ 和 $(1,1)$,因此积分区间为 $[0,1]$ 和 $[1,2]$。
步骤 2:计算平面图形 D 的面积
平面图形 D 的面积可以通过计算两个积分的和来得到,即 ${\int }_{0}^{1}(x-{x}^{2})dx+{\int }_{1}^{2}({x}^{2}-x)dx$。
步骤 3:计算平面图形 D 绕 x 轴旋转得到的旋转体体积
旋转体体积可以通过计算两个积分的和来得到,即 $\pi {\int }_{0}^{1}({x}^{2}-{x}^{4})dx+\pi {\int }_{1}^{2}({x}^{4}-{x}^{2})dx$。
曲线 $f(x) = x^2$ 与直线 $y = x$ 的交点为 $(0,0)$ 和 $(1,1)$,因此积分区间为 $[0,1]$ 和 $[1,2]$。
步骤 2:计算平面图形 D 的面积
平面图形 D 的面积可以通过计算两个积分的和来得到,即 ${\int }_{0}^{1}(x-{x}^{2})dx+{\int }_{1}^{2}({x}^{2}-x)dx$。
步骤 3:计算平面图形 D 绕 x 轴旋转得到的旋转体体积
旋转体体积可以通过计算两个积分的和来得到,即 $\pi {\int }_{0}^{1}({x}^{2}-{x}^{4})dx+\pi {\int }_{1}^{2}({x}^{4}-{x}^{2})dx$。