题目
设函数 (x)=(e)^dfrac (1{x-1)}dfrac (ln |x+2|)({x)^2+x-6}求(x)=(e)^dfrac (1{x-1)}dfrac (ln |x+2|)({x)^2+x-6} 的间断点并判断其类型
设函数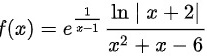 
求
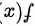的间断点并判断其类型
题目解答
答案
分析得：函数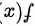在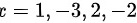
处没有定义，是间断点。
当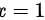
时考察
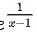
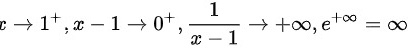
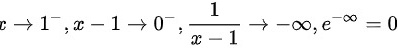
∴当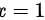时为无穷间断点
当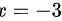
时考察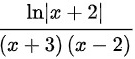
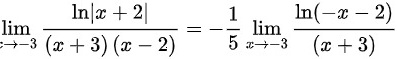
由洛必达法则得：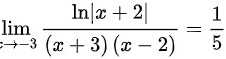
∴当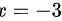时，为可去间断点
当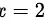
时，考察
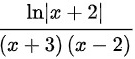
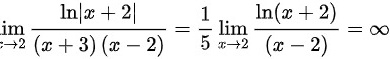
∴当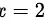时，为无穷间断点
当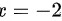
时，考察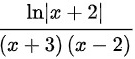
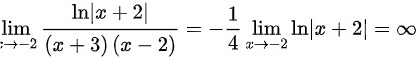
∴当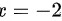时，为无穷间断点
解析
步骤 1：确定函数的定义域
函数 $f(x)={e}^{\dfrac {1}{x-1}}\dfrac {\ln |x+2|}{{x}^{2}+x-6}$ 中，分母 ${x}^{2}+x-6$ 可以分解为 $(x+3)(x-2)$，因此函数在 $x=-3$ 和 $x=2$ 处没有定义。同时，由于 $\ln |x+2|$ 的定义域为 $x \neq -2$，因此函数在 $x=-2$ 处也没有定义。此外，由于 ${e}^{\dfrac {1}{x-1}}$ 在 $x=1$ 处没有定义，因此函数在 $x=1$ 处也没有定义。所以，函数的间断点为 $x=-3$，$x=-2$，$x=1$，$x=2$。
步骤 2：判断间断点的类型
- 当 $x=1$ 时，考察 $\dfrac {1}{x-1}$ 的极限：
- 当 $x \rightarrow 1^{+}$ 时，$x-1 \rightarrow 0^{+}$，$\dfrac {1}{x-1} \rightarrow +\infty$，${e}^{+\infty}=\infty$。
- 当 $x \rightarrow 1^{-}$ 时，$x-1 \rightarrow 0^{-}$，$\dfrac {1}{x-1} \rightarrow -\infty$，${e}^{-\infty}=0$。
因此，当 $x=1$ 时，为无穷间断点。
- 当 $x=-3$ 时，考察 $\dfrac {\ln |x+2|}{(x+3)(x-2)}$ 的极限：
- $\lim _{x\rightarrow -3}\dfrac {\ln |x+2|}{(x+3)(x-2)}=-\dfrac {1}{5}\lim _{x\rightarrow -3}\dfrac {\ln (-x-2)}{(x+3)}$。
- 由洛必达法则得：$\lim _{x\rightarrow -3}\dfrac {\ln |x+2|}{(x+3)(x-2)}=\dfrac {1}{5}$。
因此，当 $x=-3$ 时，为可去间断点。
- 当 $x=2$ 时，考察 $\dfrac {\ln |x+2|}{(x+3)(x-2)}$ 的极限：
- $\lim _{x\rightarrow 2}\dfrac {\ln |x+2|}{(x+3)(x-2)}=\dfrac {1}{5}\lim _{x\rightarrow 2}\dfrac {\ln (x+2)}{(x-2)}=\infty$。
因此，当 $x=2$ 时，为无穷间断点。
- 当 $x=-2$ 时，考察 $\dfrac {\ln |x+2|}{(x+3)(x-2)}$ 的极限：
- $\lim _{x\rightarrow -2}\dfrac {\ln |x+2|}{(x+3)(x-2)}=-\dfrac {1}{4}\lim _{x\rightarrow -2}\ln |x+2|=\infty$。
因此，当 $x=-2$ 时，为无穷间断点。
函数 $f(x)={e}^{\dfrac {1}{x-1}}\dfrac {\ln |x+2|}{{x}^{2}+x-6}$ 中，分母 ${x}^{2}+x-6$ 可以分解为 $(x+3)(x-2)$，因此函数在 $x=-3$ 和 $x=2$ 处没有定义。同时，由于 $\ln |x+2|$ 的定义域为 $x \neq -2$，因此函数在 $x=-2$ 处也没有定义。此外，由于 ${e}^{\dfrac {1}{x-1}}$ 在 $x=1$ 处没有定义，因此函数在 $x=1$ 处也没有定义。所以，函数的间断点为 $x=-3$，$x=-2$，$x=1$，$x=2$。
步骤 2：判断间断点的类型
- 当 $x=1$ 时，考察 $\dfrac {1}{x-1}$ 的极限：
- 当 $x \rightarrow 1^{+}$ 时，$x-1 \rightarrow 0^{+}$，$\dfrac {1}{x-1} \rightarrow +\infty$，${e}^{+\infty}=\infty$。
- 当 $x \rightarrow 1^{-}$ 时，$x-1 \rightarrow 0^{-}$，$\dfrac {1}{x-1} \rightarrow -\infty$，${e}^{-\infty}=0$。
因此，当 $x=1$ 时，为无穷间断点。
- 当 $x=-3$ 时，考察 $\dfrac {\ln |x+2|}{(x+3)(x-2)}$ 的极限：
- $\lim _{x\rightarrow -3}\dfrac {\ln |x+2|}{(x+3)(x-2)}=-\dfrac {1}{5}\lim _{x\rightarrow -3}\dfrac {\ln (-x-2)}{(x+3)}$。
- 由洛必达法则得：$\lim _{x\rightarrow -3}\dfrac {\ln |x+2|}{(x+3)(x-2)}=\dfrac {1}{5}$。
因此，当 $x=-3$ 时，为可去间断点。
- 当 $x=2$ 时，考察 $\dfrac {\ln |x+2|}{(x+3)(x-2)}$ 的极限：
- $\lim _{x\rightarrow 2}\dfrac {\ln |x+2|}{(x+3)(x-2)}=\dfrac {1}{5}\lim _{x\rightarrow 2}\dfrac {\ln (x+2)}{(x-2)}=\infty$。
因此，当 $x=2$ 时，为无穷间断点。
- 当 $x=-2$ 时，考察 $\dfrac {\ln |x+2|}{(x+3)(x-2)}$ 的极限：
- $\lim _{x\rightarrow -2}\dfrac {\ln |x+2|}{(x+3)(x-2)}=-\dfrac {1}{4}\lim _{x\rightarrow -2}\ln |x+2|=\infty$。
因此，当 $x=-2$ 时，为无穷间断点。