题目
[题目]设A,B为n阶方阵,且满足等式 =0, 则必-|||-有() ()-|||-A. A=0 或 B=0-|||-B. A+B=0-|||-C. |A|=0 或 |B|=0-|||-D. |A|+|B|=0

题目解答
答案
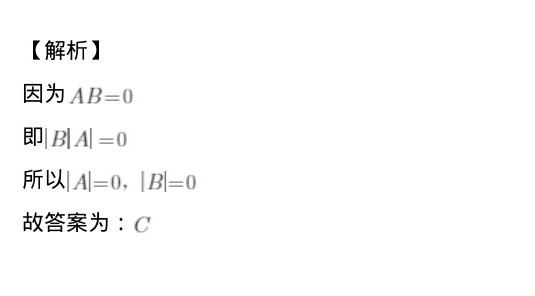
解析
考查要点:本题主要考查矩阵乘法的性质,特别是行列式的乘积性质,以及行列式为零的条件。
解题核心思路:
利用行列式的性质,若矩阵乘积$AB=0$,则$|AB|=|A||B|=0$,从而得出至少有一个矩阵的行列式为零,即$|A|=0$或$|B|=0$。需注意选项中的其他情况可能存在反例,需逐一排除。
破题关键点:
- 行列式的乘积性质:$|AB|=|A||B|$。
- 行列式为零的条件:若$|A|=0$或$|B|=0$,则矩阵$A$或$B$不可逆。
- 反例验证:通过构造非零矩阵的乘积为零的情况,排除选项A、B、D。
选项分析:
-
选项A($A=0$或$B=0$):
反例:设$A=\begin{pmatrix}1&0\\0&0\end{pmatrix}$,$B=\begin{pmatrix}0&0\\0&1\end{pmatrix}$,此时$AB=0$,但$A\neq0$且$B\neq0$。因此选项A不成立。 -
选项B($A+B=0$):
反例:若$A=\begin{pmatrix}1&0\\0&0\end{pmatrix}$,$B=\begin{pmatrix}0&0\\0&1\end{pmatrix}$,则$A+B=\begin{pmatrix}1&0\\0&1\end{pmatrix}\neq0$。因此选项B不成立。 -
选项C($|A|=0$或$|B|=0$):
由行列式的性质,$|AB|=|A||B|=0$,因此必有$|A|=0$或$|B|=0$。选项C成立。 -
选项D($|A|+|B|=0$):
反例:若$|A|=0$,$|B|=1$,则$|A|+|B|=1\neq0$。因此选项D不成立。